7.4 回溯算法

ITCharge大约 19 分钟

7.4 回溯算法

---

1. 回溯算法简介

回溯算法（Backtracking）：回溯算法是一种系统地搜索所有可能解的算法，通过递归和试错的方式逐步构建解的过程。当发现当前路径无法满足题目要求或无法得到有效解时，算法会撤销上一步的选择（即「回溯」），返回到上一个决策点，尝试其他可能的路径。回溯法的核心思想是「走不通就退回，换条路再试」，而每次需要回退的节点称为「回溯点」。

简而言之，回溯算法就是「遇到死路就回头」。

回溯算法常用递归方式实现，过程通常有两种结果：

找到一个满足条件的解；
尝试所有可能后，确认无解。

2. 从全排列问题直观理解回溯算法

以 $[1, 2, 3]$ 的全排列为例，回溯算法的核心流程如下：

首先选择第一个数字为 $1$ ：
- 接下来可选数字为 $2$ 和 $3$ 。
- 选择 $2$ 作为第二个数字，剩下只能选 $3$ ，得到排列 $[1, 2, 3]$ 。
- 回退一步，撤销 $3$ ，撤销 $2$ ，尝试 $3$ 作为第二个数字，剩下只能选 $2$ ，得到排列 $[1, 3, 2]$ 。
回退到最初，撤销 $1$ ，尝试以 $2$ 开头：
- 接下来可选数字为 $1$ 和 $3$ 。
- 选择 $1$ 作为第二个数字，剩下只能选 $3$ ，得到排列 $[2, 1, 3]$ 。
- 回退一步，撤销 $3$ ，撤销 $1$ ，尝试 $3$ 作为第二个数字，剩下只能选 $1$ ，得到排列 $[2, 3, 1]$ 。
再回退到最初，撤销 $2$ ，尝试以 $3$ 开头：
- 接下来可选数字为 $1$ 和 $2$ 。
- 选择 $1$ 作为第二个数字，剩下只能选 $2$ ，得到排列 $[3, 1, 2]$ 。
- 回退一步，撤销 $2$ ，撤销 $1$ ，尝试 $2$ 作为第二个数字，剩下只能选 $1$ ，得到排列 $[3, 2, 1]$ 。

简而言之，每次选择一个数字作为当前位置的元素，递归地选择下一个位置的数字。当所有数字都被选完时，得到一个完整的排列；如果发现当前选择无法继续，则回退到上一步，尝试其他可能性。这样就能系统地枚举出所有全排列。

全排列的回溯过程可以简要归纳为：

逐位枚举每个位置可能出现的数字，且每个数字在同一排列中只出现一次。
对于每一位，遵循以下步骤：
1. 选择元素：从当前可选的数字中，挑选一个未被使用的数字。
2. 递归探索：将该数字加入当前路径，递归进入下一层，继续选择下一个位置的数字，直到满足终止条件（如路径长度等于数组长度）。
3. 撤销选择（回溯）：递归返回后，移除刚才选择的数字，恢复现场，尝试其他未选过的数字，探索不同的分支，直到所有可能路径都被遍历。

上述决策过程可以用一棵决策树形象表示：

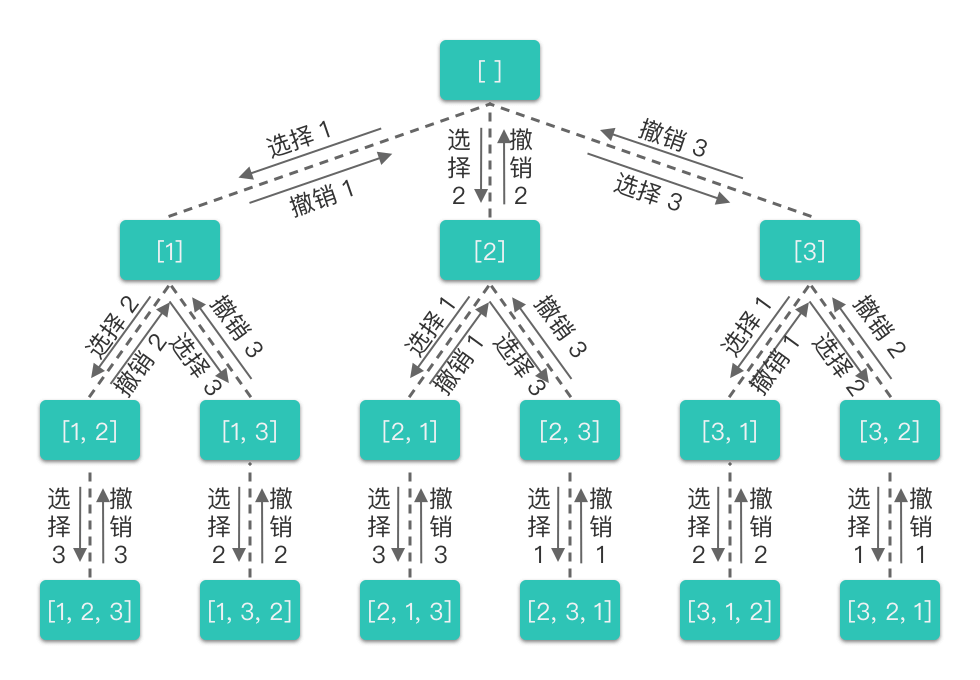
从全排列的决策树结构可以看出：

每一层代表当前递归的深度，每个节点及其分支对应一次不同的选择。
每个节点表示当前排列的一个「状态」，即已选择的数字序列。
向下递归一层，相当于在可选数字中再选一个数字加入当前状态。
当某条分支探索结束后，递归会逐层回退（回溯），撤销最近的选择，恢复到上一个状态，继续尝试其他分支。

基于上述思路和决策树结构，下面给出全排列问题的回溯算法代码（假设输入数组 $nums$ 无重复元素）：

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        """
        回溯法求解全排列问题
        :param nums: 输入的数字列表
        :return: 所有可能的全排列
        """
        res = []    # 用于存放所有符合条件的排列结果
        path = []   # 用于存放当前递归路径下的排列

        def backtracking():
            # 递归终止条件：当 path 长度等于 nums 长度时，说明找到一个完整排列
            if len(path) == len(nums):
                res.append(path[:])  # 注意要拷贝一份 path，否则后续 path 变化会影响结果
                return

            # 遍历所有可选的数字
            for i in range(len(nums)):
                if nums[i] in path:
                    # 如果当前数字已经在 path 中，跳过，保证每个数字只出现一次
                    continue
                # 做选择：将当前数字加入 path
                path.append(nums[i])
                # 递归进入下一层，继续选择下一个数字
                backtracking()
                # 撤销选择：回退到上一步，移除最后一个数字，尝试其他分支
                path.pop()

        backtracking()
        return res

3. 回溯算法通用模板

结合前文全排列问题的回溯实现，我们可以总结出一套简洁高效的回溯算法通用模板，具体如下：

res = []    # 存放所有符合条件结果的集合
path = []   # 存放当前递归路径下的结果

def backtracking(nums):
    """
    回溯算法通用模板
    :param nums: 可选元素列表
    """
    # 递归终止条件：根据具体问题设定（如 path 满足特定条件）
    if 满足结束条件:  # 例如：len(path) == len(nums)
        res.append(path[:])  # 注意要拷贝一份 path，避免后续修改影响结果
        return

    # 遍历所有可选的元素
    for i in range(len(nums)):
        # 可选：根据具体问题添加剪枝条件，如元素不能重复选取
        # if nums[i] in path:
        #     continue

        path.append(nums[i])      # 做选择，将当前元素加入 path
        backtracking(nums)        # 递归，继续选择下一个元素
        path.pop()                # 撤销选择，回退到上一步状态

# 调用回溯函数，开始搜索
backtracking(nums)

4. 回溯算法的基本步骤

回溯算法的核心思想是：通过深度优先搜索，不断尝试所有可能的选择，当发现当前路径不满足条件时就回退（回溯），尝试其他路径，最终找到所有可行解或最优解。

回溯算法的基本步骤如下：

明确所有选择：画出决策树，理清每一步有哪些可选项。每个节点的分支代表一次选择。
明确终止条件：终止条件通常是递归到某一深度、遍历完所有元素或满足题目要求。到达终止条件时，处理当前结果（如加入答案集）。
将决策树和终止条件转化为代码：
- 定义回溯函数（明确函数意义、传入参数、返回结果等）。
- 书写回溯函数主体（给出约束条件、选择元素、递归搜索、撤销选择部分）。
- 明确递归终止条件（给出递归终止条件，以及递归终止时的处理方法）。

4.1 明确所有选择

决策树是帮助我们理清搜索过程的一个很好的工具。我们可以画出搜索过程的决策树，根据决策树来帮助我们确定搜索范围和对应的搜索路径。

4.2 明确终止条件

回溯算法的终止条件，通常对应于决策树的叶子节点，即到达无法继续做选择的位置。

常见的终止条件包括：递归达到指定深度、遍历到叶子节点、遍历完所有元素等。此时需要对当前路径进行处理，例如将符合要求的结果加入答案集合，或输出当前解等。

4.3 将决策树和终止条件转化为代码

4.3.1 定义回溯函数

在定义回溯函数时，首先要清晰地界定递归函数的含义：即该函数的参数、全局变量分别代表什么，以及最终希望通过递归解决什么问题。

参数与全局变量设计：参数和全局变量应能完整表达递归过程中的「当前状态」。通常，参数用于传递当前可选的元素、已做出的选择等信息，全局变量则用于收集所有满足条件的解。

以全排列问题为例，backtracking(nums) 的参数 $nums$ 表示当前可选的元素列表，全局变量 $path$ 记录当前递归路径（已选择的元素）， $res$ 用于存储所有符合条件的结果。这样， $nums$ 反映可选空间， $path$ 反映当前状态， $res$ 汇总所有解。

返回值设计：回溯函数的返回值通常用于在递归终止时向上一层传递结果。大多数情况下，回溯函数只需返回单个节点或数值，表明当前搜索的结果。

如果采用全局变量（如 $res$ ）来收集所有解，则回溯函数可以不显式返回结果，直接 return 即可。例如全排列问题中，递归终止时将 $path$ 加入 $res$ ，无需返回值。

4.3.2 书写回溯函数主体

结合当前可选元素、题目约束（如某元素不可重复选择）、以及用于记录当前路径的变量，我们即可编写回溯函数的核心主体部分。即：

for 选择 in 可选列表:
    if 满足约束:
        做选择
        backtrack(新参数)
        撤销选择

4.3.3 明确递归终止条件

这一环节的本质，是将「4.2 明确终止条件」中分析得到的递归终止条件及其对应的处理逻辑，具体实现为代码中的判断语句和相应的操作。例如，判断是否达到递归深度或满足题目要求，并在满足时将当前结果加入答案集等。

4.3.4 回溯函数通用模板

通过上述三步分析，我们可以归纳出回溯算法的核心流程：首先枚举所有可选项，然后判断是否满足终止条件，最后递归深入，并在必要时撤销选择进行回溯。这种结构化的思考方式，使回溯算法能够高效地解决组合、排列、子集等典型问题。接下来，我们将结合具体例题，进一步体会回溯算法在实际问题中的应用与实现。

回溯通用模板如下：

def backtrack(参数):
    if 终止条件:
        处理结果
        return
    for 选择 in 可选列表:
        if 满足约束:
            做选择
            backtrack(新参数)
            撤销选择

5. 回溯算法的应用

5.1 经典例题：子集

5.1.1 题目链接

78. 子集 - 力扣（LeetCode）

5.1.2 题目大意

描述：给定一个整数数组 $nums$ ，数组中的元素互不相同。

要求：返回该数组所有可能的不重复子集。可以按任意顺序返回解集。

说明：

$1 \le nums.length \le 10$ 。
$-10 \le nums[i] \le 10$ 。
$nums$ 中的所有元素互不相同。

示例：

示例 1：

输入 nums = [1,2,3]
输出 [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

5.1.3 解题思路

思路 1：回溯算法

对于数组中的每个元素，都有「选择」或「不选择」两种可能。

我们可以通过将元素加入当前子集（path）来表示「选择」，递归结束后再将其移除（即回溯），从而实现「撤销选择」，表示「不选择」该元素。

下面结合回溯算法的三大步骤，梳理子集问题的解题思路：

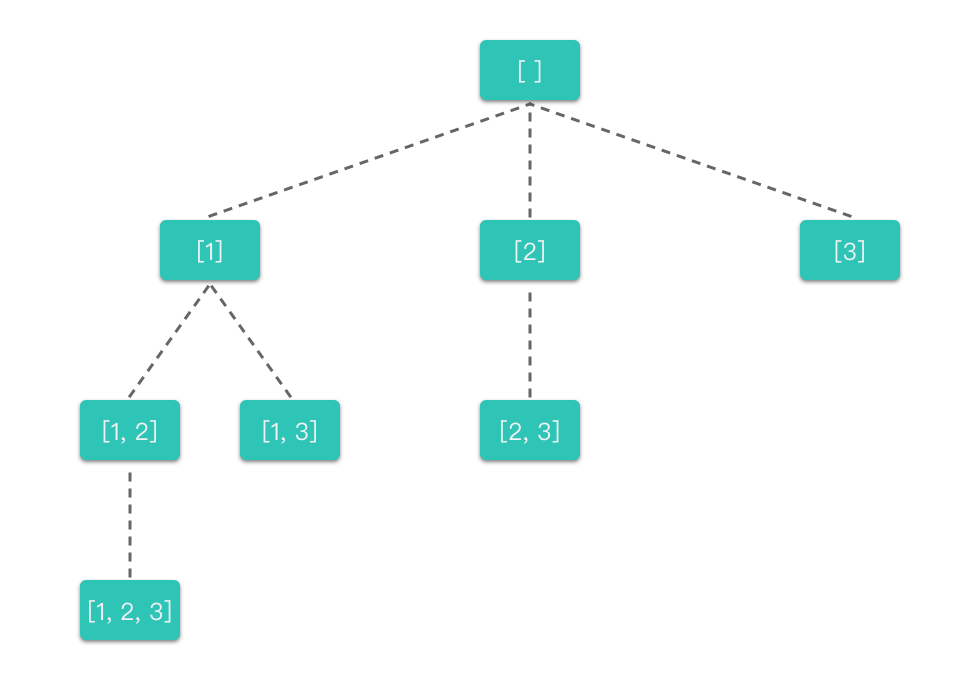
明确所有选择：对于数组的每个位置，都可以选择是否将该元素加入当前子集。决策树的每一层对应一个元素的选择与否。
明确终止条件：
- 当递归遍历到数组末尾（即所有元素都被考虑过）时，递归终止。
将思路转化为代码实现：
1. 定义回溯函数：
  - backtracking(nums, index)，其中 $nums$ 是原始数组， $index$ 表示当前递归到的元素下标。全局变量 $res$ 用于存储所有子集结果， $path$ 用于存储当前子集路径。
  - 该函数的含义是：从 $index$ 开始，依次尝试将后续元素加入子集，递归搜索所有可能的组合。
2. 编写回溯主体逻辑（选择、递归、回溯）：
  - 从 $index$ $in d e x$ 开始，依次枚举每个可选元素。对于每个元素：
    - 去重约束：每次递归都从 $index$ 开始，避免重复选择已考虑过的元素，保证子集不重复（如 {1,2} 和 {2,1} 视为同一子集）。
    - 选择：将当前元素加入 $path$ 。
    - 递归：递归进入下一层，继续选择下一个元素。
    - 回溯：递归返回后，移除刚刚加入的元素，恢复现场，尝试其他分支。
```
# 从当前下标开始，依次尝试选择每个元素
for i in range(index, len(nums)):
    path.append(nums[i])        # 选择当前元素，加入子集
    backtracking(i + 1)         # 递归，继续选择下一个元素
    path.pop()                  # 撤销选择，回溯到上一步
```
1. 明确递归终止条件及结果处理：
  - 每次进入回溯函数时，都将当前 $path$ 加入结果集 $res$ ，因为子集问题需要收集所有状态（包括中间状态和叶子节点）。
  - 当 $index \ge len(nums)$ 时，递归自然终止，无需额外处理。

简而言之，回溯法通过「选择 - 递归 - 回溯」三步，系统地枚举所有子集，并通过合理的约束避免重复。

思路 1：代码

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        """
        回溯法求解子集问题。
        :param nums: 输入数组
        :return: 所有子集的列表
        """
        res = []   # 用于存放所有子集结果
        path = []  # 用于存放当前递归路径上的子集

        def backtracking(index: int):
            """
            回溯函数，递归枚举所有子集。
            :param index: 当前递归到的元素下标
            """
            # 每次进入回溯函数，都将当前路径（子集）加入结果集
            res.append(path[:])
            # 递归终止条件：index 超过数组长度时返回
            if index >= len(nums):
                return
            # 从当前下标开始，依次尝试选择每个元素
            for i in range(index, len(nums)):
                path.append(nums[i])        # 选择当前元素，加入子集
                backtracking(i + 1)         # 递归，继续选择下一个元素
                path.pop()                  # 撤销选择，回溯到上一步

        backtracking(0)  # 从下标 0 开始递归
        return res

思路 1：复杂度分析

时间复杂度： $O(n \times 2^n)$ 。其中 $n$ 是数组 $nums$ 的元素个数。回溯过程中，每个元素有选与不选两种状态，共 $2^n$ 种子集，每生成一个子集需要 $O(n)$ 的时间（因为要拷贝 path 到结果集）。
空间复杂度： $O(n)$ 。递归过程中 path 最深为 $n$ ，递归栈空间也是 $O(n)$ 。

5.2 N 皇后

5.2.1 题目链接

51. N 皇后 - 力扣（LeetCode）

5.2.2 题目大意

描述：给定一个整数 $n$ 。

要求：返回所有不同的「 $n$ 皇后问题」的解决方案。每一种解法包含一个不同的「 $n$ 皇后问题」的棋子放置方案，该方案中的 Q 和 . 分别代表了皇后和空位。

说明：

n 皇后问题：将 $n$ 个皇后放置在 $n \times n$ 的棋盘上，并且使得皇后彼此之间不能攻击。
皇后彼此不能相互攻击：指的是任何两个皇后都不能处于同一条横线、纵线或者斜线上。
$1 \le n \le 9$ 。

示例：

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如下图所示，4 皇后问题存在 2 个不同的解法。

5.2.3 解题思路

思路 1：回溯算法

本题是回溯算法的经典应用。我们按照「逐行放置皇后」的顺序进行搜索：即先在第 1 行放皇后，再到第 2 行，依次递归，直到最后一行。

对于 $n \times n$ 的棋盘，每一行有 $n$ 个位置可选。每次尝试将皇后放在当前行的某一列，并判断该位置是否与之前已放置的皇后冲突（即是否在同一列、主对角线、副对角线上）。如果不冲突，则递归进入下一行继续放置；若冲突，则跳过该位置，尝试下一列。所有皇后都成功放置后，即得到一个有效解。回溯算法会自动探索所有可能的分支，确保所有解都被枚举。

下面结合回溯算法的“三步走”思想，梳理 N 皇后问题的解题流程：

明确所有选择：对于当前行，依次尝试将皇后放在每一列的不同位置，每个位置都代表一次选择，整个过程可用决策树表示（如上图）。
明确终止条件：
- 当所有行都已成功放置皇后（即递归到第 $n$ 行），说明找到一个有效解，此时递归终止。
将决策树和终止条件转化为代码实现：
1. 定义回溯函数：
  - 使用一个 $n \times n$ 的二维数组 $chessboard$ 表示棋盘，Q 表示皇后，. 表示空位，初始均为 .。
  - 定义回溯函数 backtrack(chessboard, row)，其中 $chessboard$ 为当前棋盘状态， $row$ 表示当前正在处理的行，全局变量 $res$ 用于收集所有可行解。
  - backtrack(chessboard, row) 的含义是：在前 $row-1$ 行已放置皇后的前提下，递归尝试为第 $row$ 行放置皇后。
2. 编写回溯函数主体（包括选择、递归、撤销选择）：
  - 遍历当前行的每一列，对于每个位置：
    - 约束条件：通过辅助函数判断当前位置是否与已放置的皇后冲突，若无冲突则继续，否则跳过。
    - 选择：在 $row, col$ 位置放置皇后（即 $chessboard[row][col] = 'Q'$ ）。
    - 递归：递归处理下一行（ $row+1$ ）。
    - 撤销选择：回溯时将 $chessboard[row][col]$ 恢复为 .，以便尝试其他方案。
```
# 枚举当前行的每一列，尝试放置皇后
for col in range(n):
    if self.isValid(n, row, col, chessboard):  # 检查当前位置是否合法
        chessboard[row][col] = 'Q'  # 放置皇后
        self.backtrack(n, row + 1, chessboard)  # 递归处理下一行
        chessboard[row][col] = '.'  # 撤销选择，回溯
```
1. 明确递归终止条件（即何时递归应当结束，以及结束时如何处理结果）。
  - 当递归到第 $n$ 行（即 $row == n$ ）时，说明所有皇后已成功放置，此时到达决策树的叶子节点，递归终止。
  - 终止时，将当前棋盘状态转换为题目要求的格式，并加入结果集 $res$ 。

思路 1：代码

class Solution:
    res = []  # 用于存储所有可行解

    def backtrack(self, n: int, row: int, chessboard: List[List[str]]):
        """
        回溯主函数：在第 row 行尝试放置皇后
        :param n: 棋盘大小（n x n）
        :param row: 当前递归到的行号
        :param chessboard: 当前棋盘状态
        """
        if row == n:
            # 递归终止条件：所有行都已放置皇后，记录当前棋盘方案
            temp_res = []
            for temp in chessboard:
                temp_str = ''.join(temp)  # 将每一行转为字符串
                temp_res.append(temp_str)
            self.res.append(temp_res)
            return
        # 枚举当前行的每一列，尝试放置皇后
        for col in range(n):
            if self.isValid(n, row, col, chessboard):  # 检查当前位置是否合法
                chessboard[row][col] = 'Q'  # 放置皇后
                self.backtrack(n, row + 1, chessboard)  # 递归处理下一行
                chessboard[row][col] = '.'  # 撤销选择，回溯

    def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]):
        """
        检查在 (row, col) 位置放置皇后是否合法
        :param n: 棋盘大小
        :param row: 当前行
        :param col: 当前列
        :param chessboard: 当前棋盘状态
        :return: True 表示合法，False 表示冲突
        """
        # 检查同一列是否有皇后
        for i in range(row):
            if chessboard[i][col] == 'Q':
                return False

        # 检查左上对角线是否有皇后
        i, j = row - 1, col - 1
        while i >= 0 and j >= 0:
            if chessboard[i][j] == 'Q':
                return False
            i -= 1
            j -= 1

        # 检查右上对角线是否有皇后
        i, j = row - 1, col + 1
        while i >= 0 and j < n:
            if chessboard[i][j] == 'Q':
                return False
            i -= 1
            j += 1

        return True  # 没有冲突，可以放置

    def solveNQueens(self, n: int) -> List[List[str]]:
        """
        主入口函数，返回所有 N 皇后问题的解
        :param n: 棋盘大小
        :return: 所有可行解的列表
        """
        self.res.clear()  # 清空历史结果
        # 初始化棋盘，全部填充为 '.'
        chessboard = [['.' for _ in range(n)] for _ in range(n)]
        self.backtrack(n, 0, chessboard)  # 从第 0 行开始回溯
        return self.res

思路 1：复杂度分析

时间复杂度： $O(n!)$ ，其中 $n$ 是皇后数量。
空间复杂度： $O(n^2)$ ，其中 $n$ 是皇后数量。递归调用层数不会超过 $n$ ，每个棋盘的空间复杂度为 $O(n^2)$ ，所以空间复杂度为 $O(n^2)$ 。

6. 总结

回溯算法是一种通过递归和试错来系统地搜索所有可能解的算法。其核心思想是「走不通就退回，换条路再试」，通过深度优先搜索的方式遍历决策树，当发现当前路径无法满足条件时，会撤销上一步的选择并尝试其他可能性。

回溯算法的关键在于「选择 - 递归 - 回溯」：首先做出选择，然后递归进入下一层继续搜索，最后在递归返回时撤销选择，恢复到之前的状态。这种机制使得算法能够穷尽所有可能的解空间，特别适用于需要枚举所有可能解的问题。

回溯算法在解决组合、排列、子集等经典问题中表现出色，如全排列、N皇后、子集生成等。其通用模板简洁明了，通过明确所有选择、确定终止条件、转化为代码实现三个步骤，可以高效地解决各种回溯类问题。

虽然回溯算法能够保证找到所有解，但其时间复杂度通常较高，特别是在解空间较大时。因此，在实际应用中需要结合剪枝等优化技巧来提高效率，避免不必要的搜索路径。

练习题目

参考资料

【题解】回溯算法入门级详解 + 练习（持续更新） - 全排列 - 力扣
【题解】「代码随想录」带你学透回溯算法！51. N-Queens - N 皇后 - 力扣
【文章】回溯算法详解
【文章】回溯算法详解修订版 - labuladong
【文章】【算法】回溯法四步走 - Nemo& - 博客园