跳至主要內容

7.5 贪心算法

ITCharge大约 12 分钟

7.5 贪心算法

---

1. 贪心算法简介

1.1 贪心算法的定义

贪心算法（Greedy Algorithm）：每一步都选择当前最优（看起来最好的）方案，期望通过一系列局部最优，最终获得全局最优解。

贪心算法的核心思想是：将问题分解为若干步骤，每一步都根据当前情况，按照某种标准选择最优解（即「贪心」选择），不回头、不考虑整体，只关注当前最优。这样可以避免穷举所有可能，大大简化求解过程。

简而言之，贪心算法每次只做出当前看来最优的选择，期望通过一系列这样的选择得到整体最优解。

1.2 贪心算法的特征

贪心算法适用于一类特殊问题：只要每一步都做出当前最优选择，最终就能得到整体最优解或近似最优解。但并非所有问题都适用贪心算法。

通常，能用贪心算法解决的问题需同时满足两个条件：

  1. 贪心选择性质
  2. 最优子结构

1.2.1 贪心选择性质

贪心选择性质：全局最优解可以通过一系列局部最优（贪心）选择获得。

也就是说，每次只需关注当前最优选择，无需关心子问题的解。做出选择后，再递归处理剩下的子问题。

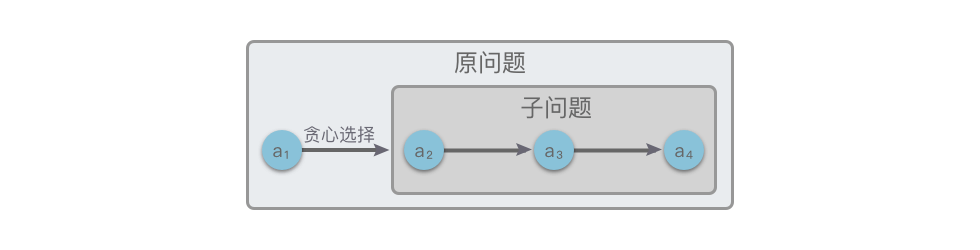
贪心选择性质
贪心选择性质

贪心算法的每一步可能依赖之前的选择，但不会回溯，也不依赖未来的选择或子问题的解。

1.2.2 最优子结构性质

最优子结构性质：问题的最优解包含其子问题的最优解。

这是贪心算法成立的关键。举例来说，假设原问题 S={a1,a2,a3,a4}S = \lbrace a_1, a_2, a_3, a_4 \rbrace，第一步通过贪心选择得到当前最优解，剩下的子问题 S子问题={a2,a3,a4}S_{\text{子问题}} = \lbrace a_2, a_3, a_4 \rbrace。如果原问题的最优解等于「当前贪心选择」加上「子问题的最优解」，则满足最优子结构。

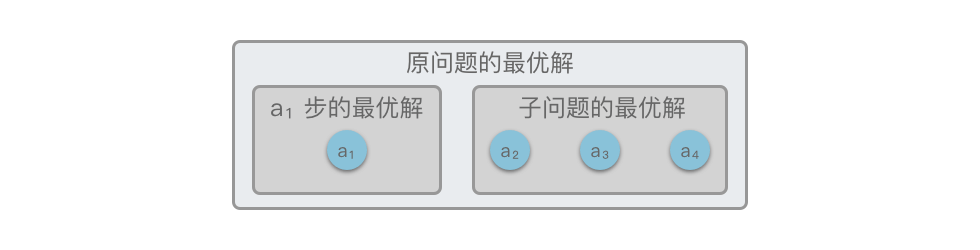
最优子结构性质
最优子结构性质

如果原问题的最优解可以由子问题的最优解推导出来，则说明满足最优子结构；反之，则不满足，不能用贪心算法。

1.3 贪心算法正确性简述

贪心算法的难点在于如何证明其选择策略能得到全局最优解。常见的两种证明方法：

  • 数学归纳法：先验证最小规模（如 n=1n = 1）时成立，再证明 nn 成立时 n+1n + 1 也成立。
  • 交换论证法：假设存在更优解，通过交换局部选择，如果不会得到更优结果，则当前贪心解为最优。

实际刷题或面试时，通常不要求严格证明。判断是否可用贪心算法，可以通过：

  1. 直觉尝试：先用贪心思路做一遍，看看局部最优能否推出全局最优。
  2. 举反例：尝试构造反例，如果找不到局部最优导致全局最优失败的例子，基本可以用贪心法。

2. 贪心算法三步走

  1. 问题转化：将原始优化问题转化为可以应用贪心策略的问题，明确每一步都可以做出一个局部最优的选择。
  2. 贪心策略制定：结合题意，选定合适的度量标准，设计出每一步的贪心选择规则，即在当前状态下选择最优（最有利）的方案，获得局部最优解。
  3. 最优子结构利用：保证每次贪心选择后，剩余子问题仍满足同样的结构和贪心选择性质，将每一步的局部最优解累积，最终合成原问题的全局最优解。

3. 贪心算法的应用

3.1 经典例题：分发饼干

3.1.1 题目链接

3.1.2 题目大意

描述：一位很棒的家长为孩子们分发饼干。对于每个孩子 ii，都有一个胃口值 g[i]g[i]，即每个小孩希望得到饼干的最小尺寸值。对于每块饼干 jj，都有一个尺寸值 s[j]s[j]。只有当 s[j]>g[i]s[j] > g[i] 时，我们才能将饼干 jj 分配给孩子 ii。每个孩子最多只能给一块饼干。

现在给定代表所有孩子胃口值的数组 gg 和代表所有饼干尺寸的数组 jj。

要求：尽可能满足越多数量的孩子，并求出这个最大数值。

说明：

  • 1≤g.length≤3∗1041 \le g.length \le 3 * 10^4。
  • 0≤s.length≤3∗1040 \le s.length \le 3 * 10^4。
  • 1≤g[i],s[j]≤231−11 \le g[i], s[j] \le 2^{31} - 1。

示例：

  • 示例 1：
输入：g = [1,2,3], s = [1,1]
输出：1
解释：你有三个孩子和两块小饼干，3 个孩子的胃口值分别是：1, 2, 3。虽然你有两块小饼干，由于他们的尺寸都是 1，你只能让胃口值是 1 的孩子满足。所以应该输出 1。
  • 示例 2：
输入: g = [1,2], s = [1,2,3]
输出: 2
解释: 你有两个孩子和三块小饼干，2个孩子的胃口值分别是1, 2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2。

3.1.3 解题思路

思路 1：贪心算法

为了让尽可能多的孩子得到满足，且每块饼干只能分配给一个孩子，我们应优先用小尺寸的饼干满足胃口较小的孩子，将大尺寸的饼干留给胃口较大的孩子。

基于贪心思想，具体做法如下：先将孩子的胃口数组 gg 和饼干尺寸数组 ss 分别从小到大排序。然后，依次为每个孩子分配能够满足其胃口的最小尺寸饼干。

结合贪心算法的三步走：

  1. 问题转化：将原问题转化为：每次优先用最小的饼干满足胃口最小的孩子，剩下的孩子和饼干继续按同样方式处理（即递归到子问题）。
  2. 贪心选择性质：对于当前孩子，选择能满足其胃口的最小饼干。
  3. 最优子结构：当前的贪心选择加上剩余子问题的最优解，能够保证全局最优，即最大化被满足的孩子数量。

具体实现步骤如下：

  1. 对 gg 和 ss 升序排序，定义指针 index_gindex\_g 和 index_sindex\_s 分别指向 gg 和 ss 的起始位置，结果计数 resres 初始化为 00。
  2. 遍历两个数组，比较 g[index_g]g[index\_g] 和 s[index_s]s[index\_s]：
    1. 如果 g[index_g]≤s[index_s]g[index\_g] \le s[index\_s]，说明当前饼干可以满足当前孩子，resres 加 11，index_gindex\_g 和 index_sindex\_s 同时右移。
    2. 如果 g[index_g]>s[index_s]g[index\_g] > s[index\_s]，说明当前饼干无法满足当前孩子，index_sindex\_s 右移，尝试下一块饼干。
  3. 遍历结束后，输出 resres 即为最多能满足的孩子数量。
思路 1：代码
class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        # 对孩子的胃口值和饼干尺寸进行升序排序
        g.sort()
        s.sort()
        index_g, index_s = 0, 0  # index_g 指向当前要分配的孩子，index_s 指向当前可用的饼干
        res = 0  # 记录能满足的孩子数量
        # 遍历两个数组，直到有一个数组遍历完
        while index_g < len(g) and index_s < len(s):
            # 如果当前饼干可以满足当前孩子
            if g[index_g] <= s[index_s]:
                res += 1  # 满足的孩子数加一
                index_g += 1  # 指向下一个孩子
                index_s += 1  # 指向下一个饼干
            else:
                index_s += 1   # 当前饼干太小，尝试下一块饼干

        return res  # 返回最多能满足的孩子数量
思路 1：复杂度分析
  • 时间复杂度：O(m×log⁡m+n×log⁡n)O(m \times \log m + n \times \log n)，其中 mm 和 nn 分别是数组 gg 和 ss 的长度。
  • 空间复杂度：O(log⁡m+log⁡n)O(\log m + \log n)。

3.2 经典例题：无重叠区间

3.2.1 题目链接

3.2.2 题目大意

描述：给定一个区间的集合 intervalsintervals，其中 intervals[i]=[starti,endi]intervals[i] = [starti, endi]。从集合中移除部分区间，使得剩下的区间互不重叠。

要求：返回需要移除区间的最小数量。

说明：

  • 1≤intervals.length≤1051 \le intervals.length \le 10^5。
  • intervals[i].length==2intervals[i].length == 2。
  • −5∗104≤starti<endi≤5∗104-5 * 10^4 \le starti < endi \le 5 * 10^4。

示例：

  • 示例 1：
输入：intervals = [[1,2],[2,3],[3,4],[1,3]]
输出：1
解释：移除 [1,3] 后，剩下的区间没有重叠。
  • 示例 2：
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

3.2.3 解题思路

思路 1：贪心算法

本题可以通过转换思路来简化求解。原题要求移除最少数量的区间，使得剩余区间互不重叠。换句话说，就是要让剩下的互不重叠区间数量最多。因此，答案等价于「总区间数 - 最多不重叠区间数」。问题转化为：在所有区间中，最多能选出多少个互不重叠的区间。

采用贪心算法时，核心策略是将区间按结束时间从小到大排序。每次总是选择结束时间最早且不与已选区间重叠的区间，这样可以在后续留出更多空间，选出更多区间。

具体贪心解题步骤如下：

  1. 问题转化：将原问题转化为「选出最多不重叠区间」。
  2. 贪心选择性质：每次总是选择当前结束时间最早且不与已选区间重叠的区间。
  3. 最优子结构性质：当前选择加上后续子问题的最优解，能够得到全局最优解。

实现流程如下：

  1. 先将所有区间按结束坐标升序排序。
  2. 维护两个变量：end_posend\_pos 表示当前已选区间的结束位置，countcount 表示已选的不重叠区间数量。初始时，end_posend\_pos 取第一个区间的结束位置，count=1count=1。
  3. 遍历后续区间，对于每个区间 intervals[i]intervals[i]：
    • 若 end_pos≤intervals[i][0]end\_pos \le intervals[i][0]，说明该区间与前面已选区间不重叠，则计数 count+1count+1，并更新 end_posend\_pos 为当前区间的结束位置。
  4. 最终返回 len(intervals)−countlen(intervals) - count，即最少需要移除的区间数。
思路 1：代码
class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        # 如果区间列表为空，直接返回 0
        if not intervals:
            return 0
        # 按区间的结束位置从小到大排序
        intervals.sort(key=lambda x: x[1])
        # 初始化第一个区间的结束位置
        end_pos = intervals[0][1]
        # 记录不重叠区间的数量，初始为 1（第一个区间）
        count = 1
        # 遍历后续区间
        for i in range(1, len(intervals)):
            # 如果当前区间的起始位置不小于上一个已选区间的结束位置，说明不重叠
            if end_pos <= intervals[i][0]:
                count += 1  # 计数加一
                end_pos = intervals[i][1]  # 更新当前已选区间的结束位置

        # 总区间数减去最多不重叠区间数，即为最少需要移除的区间数
        return len(intervals) - count
思路 1：复杂度分析
  • 时间复杂度：O(n×log⁡n)O(n \times \log n)，其中 nn 是区间的数量。
  • 空间复杂度：O(log⁡n)O(\log n)。

4. 总结

贪心算法是一种简单而有效的算法设计策略，其核心思想是在每一步都做出当前看起来最优的选择，期望通过一系列局部最优选择最终获得全局最优解。这种算法特别适用于具有贪心选择性质和最优子结构性质的问题。

贪心算法的优势在于其简洁性和高效性。相比动态规划需要存储和计算所有子问题的解，贪心算法只需要关注当前步骤的最优选择，大大降低了时间和空间复杂度。同时，贪心算法的实现通常比较简单直观，容易理解和编码。

然而，贪心算法也有其局限性。并非所有问题都适合使用贪心策略，只有同时满足贪心选择性质和最优子结构性质的问题才能保证得到全局最优解。对于不满足这些条件的问题，贪心算法可能只能得到局部最优解或近似解。此外，贪心算法的正确性证明往往比较复杂，需要严格的数学证明。

在实际应用中，贪心算法广泛应用于调度问题、图论问题、优化问题等领域。通过合理设计贪心策略，可以在保证解的质量的同时，显著提高算法的执行效率。掌握贪心算法的关键在于理解其适用条件，学会识别问题特征，并能够设计出合适的贪心选择策略。

练习题目

参考资料

本站总访问量  次 | 您是本站第  位访问者
Copyright © 2025 ITCharge