8.3 线性 DP（一）: 单串线性 DP

ITCharge大约 12 分钟

8.3 线性 DP（一）: 单串线性 DP

---

1. 线性动态规划简介

线性动态规划（线性 DP）：指的是将问题的阶段按线性顺序划分，并基于此进行状态转移的动态规划方法。如下图所示：

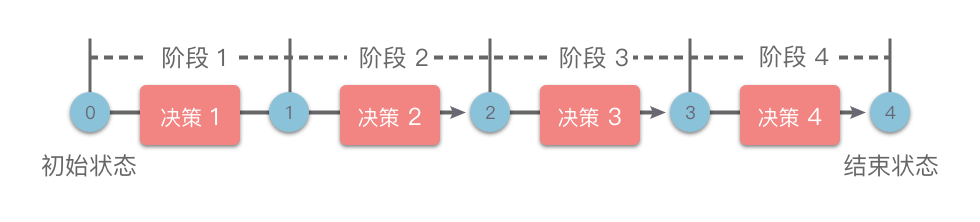
即使状态有多个维度，只要每个维度的阶段划分都是线性的，也属于线性 DP。例如，背包问题、区间 DP、数位 DP 等都属于线性 DP 的范畴。

线性 DP 问题的分类方式主要有两种：

按「状态维度」划分：可分为一维线性 DP、二维线性 DP 和多维线性 DP。
按「问题的输入格式」划分：可分为单串线性 DP、双串线性 DP、矩阵线性 DP 以及无串线性 DP。

本文将以「问题的输入格式」的方式进行分类，系统讲解线性 DP 的各类典型问题。

2. 单串线性 DP 问题简介

单串线性 DP：指输入为单个数组或字符串的线性动态规划问题。常见的状态定义为 $dp[i]$ ，其含义通常有以下三种：
以 $nums[i]$ 结尾的子数组（ $nums[0]$ 到 $nums[i]$ ， $0 \leq i < n$ ）的相关解；
以 $nums[i - 1]$ 结尾的子数组（ $nums[0]$ 到 $nums[i - 1]$ ， $1 \leq i \leq n$ ）的相关解；
由前 $i$ 个元素组成的子数组（ $nums[0]$ 到 $nums[i - 1]$ ， $1 \leq i \leq n$ ）的相关解。

这三种状态定义的主要区别在于是否包含第 $i$ 个元素 $nums[i]$ 。

第 1 种状态：子数组长度为 $i + 1$ ，不可为空；
第 2、3 种状态：本质等价，子数组长度为 $i$ ，允许为空（当 $i = 0$ 时表示空数组，便于初始化和边界处理）。

3. 单串线性 DP 问题经典题目

3.1 经典例题：最长递增子序列

单串线性 DP 问题中最经典的问题就是「最长递增子序列（Longest Increasing Subsequence，简称 LIS）」。

3.1.2 题目大意

描述：给定一个整数数组 $nums$ 。

要求：找到其中最长严格递增子序列的长度。

说明：

子序列：由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如， $[3,6,2,7]$ 是数组 $[0,3,1,6,2,2,7]$ 的子序列。
$1 \le nums.length \le 2500$ 。
$-10^4 \le nums[i] \le 10^4$ 。

示例：

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

3.1.3 解题思路

思路 1：动态规划

3. 状态转移方程

对于每个位置 $i$ ，我们需要考虑所有在 $i$ 之前的元素 $j$ （ $0 \le j < i$ ）。

如果 $nums[j] < nums[i]$ ，说明 $nums[i]$ 可以接在以 $nums[j]$ 结尾的递增子序列后面，从而形成更长的递增子序列。此时，更新 $dp[i]$ 为 $dp[i] = \max(dp[i], dp[j] + 1)$ 。
如果 $nums[j] \ge nums[i]$ ，则 $nums[i]$ 不能接在 $nums[j]$ 后面，无需更新。

因此，状态转移方程为： $dp[i] = \max(dp[i], dp[j] + 1)$ ，其中 $0 \le j < i$ 且 $nums[j] < nums[i]$ 。

4. 初始条件

每个元素自身都可以作为长度为 $1$ 的递增子序列，即 $dp[i] = 1$ 。

5. 最终结果

最终答案为 $dp$ 数组中的最大值，即 $\max(dp)$ ，表示整个数组的最长递增子序列长度。

思路 1：动态规划代码

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        size = len(nums)
        dp = [1 for _ in range(size)]

        for i in range(size):
            for j in range(i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
        
        return max(dp)

思路 1：复杂度分析

时间复杂度： $O(n^2)$ 。外层和内层循环各遍历一次数组，整体为 $O(n^2)$ ，最后取最大值为 $O(n)$ ，因此总时间复杂度为 $O(n^2)$ 。
空间复杂度： $O(n)$ 。仅需一个长度为 $n$ 的一维数组存储状态，故空间复杂度为 $O(n)$ 。

3.2 经典例题：最大子数组和

在线性 DP 问题中，除了关注子序列相关的线性 DP，还常常遇到子数组相关的线性 DP 问题。

注意区分：
子序列：从原数组中按顺序选取若干元素（可以不连续），只要不改变元素的相对顺序即可。
子数组：原数组中一段连续的元素组成的序列。
两者都是原数组的部分内容，且都保持元素的原有顺序。区别在于，子数组要求元素连续，而子序列则不要求连续。

3.2.2 题目大意

描述：给定一个整数数组 $nums$ 。

要求：找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

说明：

子数组：指的是数组中的一个连续部分。
$1 \le nums.length \le 10^5$ 。
$-10^4 \le nums[i] \le 10^4$ 。

示例：

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6。

示例 2：

输入：nums = [1]
输出：1

3.2.3 解题思路

思路 1：动态规划

1. 阶段划分

以连续子数组的「结尾位置」为阶段。即每一阶段对应以第 $i$ 个元素结尾的子数组。

3. 状态转移方程

对于第 $i$ 个元素，考虑两种情况：

如果 $dp[i - 1] < 0$ ，说明以 $i - 1$ 结尾的子数组对当前元素有负贡献，此时不如从当前元素重新开始，即 $dp[i] = nums[i]$ 。
如果 $dp[i - 1] \ge 0$ ，则以 $i - 1$ 结尾的子数组对当前元素有正贡献，可以将其累加，即 $dp[i] = dp[i-1] + nums[i]$ 。

因此，状态转移方程为：

dp[i] = \begin{cases} nums[i], & dp[i - 1] < 0 \\ dp[i-1] + nums[i], & dp[i-1] \ge 0 \end{cases}

4. 初始条件

以第 $0$ 个元素结尾的最大和为 $nums[0]$ ，即 $dp[0] = nums[0]$ 。

思路 1：代码

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        dp = [0 for _ in range(size)]

        dp[0] = nums[0]
        for i in range(1, size):
            if dp[i - 1] < 0:
                dp[i] = nums[i]
            else:
                dp[i] = dp[i - 1] + nums[i]
        return max(dp)

思路 1：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 为数组 $nums$ 的元素个数。
空间复杂度： $O(n)$ 。

思路 2：动态规划 + 滚动优化

由于 $dp[i]$ 仅依赖于 $dp[i - 1]$ 和当前元素 $nums[i]$ ，因此可以用一个变量 $subMax$ 表示以第 $i$ 个元素结尾的连续子数组的最大和，同时用 $ansMax$ 记录全局的最大子数组和，从而实现空间优化。

思路 2：代码

class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        size = len(nums)
        subMax = nums[0]
        ansMax = nums[0]

        for i in range(1, size):
            if subMax < 0:
                subMax = nums[i]
            else:
                subMax += nums[i]
            ansMax = max(ansMax, subMax)
        return ansMax

思路 2：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 为数组 $nums$ 的元素个数。
空间复杂度： $O(1)$ 。

3.3 经典例题：最长的斐波那契子序列的长度

在某些单串线性 DP 问题中，单独用一个结束位置来定义状态无法完整刻画问题，此时需要同时考虑两个结束位置，将状态定义为以这两个位置结尾，从而引入额外的维度。

3.3.2 题目大意

描述：给定一个严格递增的正整数数组 $arr$ 。

要求：从数组 $arr$ 中找出最长的斐波那契式的子序列的长度。如果不存斐波那契式的子序列，则返回 0。

说明：

斐波那契式序列：如果序列 $X_1, X_2, ..., X_n$ 满足：
- $n \ge 3$ ；
- 对于所有 $i + 2 \le n$ ，都有 $X_i + X_{i+1} = X_{i+2}$ 。
则称该序列为斐波那契式序列。
斐波那契式子序列：从序列 $A$ 中挑选若干元素组成子序列，并且子序列满足斐波那契式序列，则称该序列为斐波那契式子序列。例如： $A = [3, 4, 5, 6, 7, 8]$ 。则 $[3, 5, 8]$ 是 $A$ 的一个斐波那契式子序列。
- $3 \le arr.length \le 1000$ 。
- $1 \le arr[i] < arr[i + 1] \le 10^9$ 。

示例：

示例 1：

输入: arr = [1,2,3,4,5,6,7,8]
输出: 5
解释: 最长的斐波那契式子序列为 [1,2,3,5,8]。

示例 2：

输入: arr = [1,3,7,11,12,14,18]
输出: 3
解释: 最长的斐波那契式子序列有 [1,11,12]、[3,11,14] 以及 [7,11,18]。

3.3.3 解题思路

思路 1：暴力枚举（超时）

假设 $arr[i]$ 、 $arr[j]$ 、 $arr[k]$ 是数组 $arr$ 中的三个元素，且满足 $arr[i] + arr[j] = arr[k]$ ，那么 $arr[i]$ 、 $arr[j]$ 、 $arr[k]$ 就组成了一个斐波那契式子序列。

已知 $arr[i]$ 和 $arr[j]$ 后，下一个斐波那契式子序列的元素应为 $arr[i] + arr[j]$ 。

由于 $arr$ 是严格递增的，我们可以在确定 $arr[i]$ 和 $arr[j]$ 后，从 $j + 1$ 开始，依次查找是否存在值为 $arr[i] + arr[j]$ 的元素。如果找到了，就继续向后查找下一个元素（即前两个元素分别为 $arr[j]$ 和 $arr[k]$ ，下一个应为 $arr[j] + arr[k]$ ），以此类推，直到无法继续为止。

简而言之，每次固定一对 $arr[i]$ 和 $arr[j]$ ，就可以从这对出发，尽可能延长斐波那契式子序列，并记录其长度。遍历所有可能的 $arr[i]$ 和 $arr[j]$ 组合，统计所有斐波那契式子序列的长度，最终取最大值作为答案。

思路 1：代码

class Solution:
    def lenLongestFibSubseq(self, arr: List[int]) -> int:
        size = len(arr)
        ans = 0
        for i in range(size):
            for j in range(i + 1, size):
                temp_ans = 0
                temp_i = i
                temp_j = j
                k = j + 1
                while k < size:
                    if arr[temp_i] + arr[temp_j] == arr[k]:
                        temp_ans += 1
                        temp_i = temp_j
                        temp_j = k
                    k += 1
                if temp_ans > ans:
                    ans = temp_ans

        if ans > 0:
            return ans + 2
        else:
            return ans

思路 1：复杂度分析

时间复杂度： $O(n^3)$ ，其中 $n$ 为数组 $arr$ 的元素个数。
空间复杂度： $O(1)$ 。

对于每一对 $arr[i]$ 和 $arr[j]$ ，我们需要判断 $arr[i] + arr[j]$ 是否存在于数组 $arr$ 中。为此，可以提前构建一个哈希表，将 $arr$ 中的每个元素值映射到其下标（即 $value : idx$ ）。这样，在查找 $arr[i] + arr[j]$ 是否存在时，只需 $O(1)$ 的时间即可定位到对应的 $arr[k]$ ，无需像暴力做法那样进行线性遍历，大大提升了查找效率。

思路 2：代码

class Solution:
    def lenLongestFibSubseq(self, arr: List[int]) -> int:
        size = len(arr)
        ans = 0
        idx_map = dict()
        for idx, value in enumerate(arr):
            idx_map[value] = idx
        
        for i in range(size):
            for j in range(i + 1, size):
                temp_ans = 0
                temp_i = i
                temp_j = j
                while arr[temp_i] + arr[temp_j] in idx_map:
                    temp_ans += 1
                    k = idx_map[arr[temp_i] + arr[temp_j]]
                    temp_i = temp_j
                    temp_j = k

                if temp_ans > ans:
                    ans = temp_ans

        if ans > 0:
            return ans + 2
        else:
            return ans

思路 2：复杂度分析

时间复杂度： $O(n^2)$ ，其中 $n$ 为数组 $arr$ 的元素个数。
空间复杂度： $O(n)$ 。

补充说明：状态转移时应结合哈希表优化，快速判断 $arr[i] + arr[j]$ 是否存在于数组中，以提升效率。

思路 3：代码

class Solution:
    def lenLongestFibSubseq(self, arr: List[int]) -> int:
        size = len(arr)
        
        dp = [[0 for _ in range(size)] for _ in range(size)]
        ans = 0

        # 初始化 dp
        for i in range(size):
            for j in range(i + 1, size):
                dp[i][j] = 2

        idx_map = {}
        # 将 value : idx 映射为哈希表，这样可以快速通过 value 获取到 idx
        for idx, value in enumerate(arr):
            idx_map[value] = idx

        for i in range(size):
            for j in range(i + 1, size):
                if arr[i] + arr[j] in idx_map:    
                    # 获取 arr[i] + arr[j] 的 idx，即斐波那契式子序列下一项元素
                    k = idx_map[arr[i] + arr[j]]
                    
                    dp[j][k] = max(dp[j][k], dp[i][j] + 1)
                    ans = max(ans, dp[j][k])

        if ans >= 3:
            return ans
        return 0

思路 3：复杂度分析

时间复杂度： $O(n^2)$ ，其中 $n$ 为数组 $arr$ 的元素个数。
空间复杂度： $O(n)$ 。

练习题目

参考资料

【书籍】算法竞赛进阶指南
【文章】动态规划概念和基础线性DP | 潮汐朝夕