0085. 最大矩形

ITCharge大约 3 分钟

---

0085. 最大矩形

标签：栈、数组、动态规划、矩阵、单调栈
难度：困难

题目链接

0085. 最大矩形 - 力扣

题目大意

描述：

给定一个仅包含 $0$ 和 $1$ 、大小为 $rows \times cols$ 的二维二进制矩阵。

要求：

找出只包含 $1$ 的最大矩形，并返回其面积。

说明：

$rows == matrix$ .length$。
$cols == matrix$ [0].length$。
$1 \le row, cols \le 200$ 。
$matrix[i][j]$ 为 '0' 或 '1'。

示例：

示例 1：

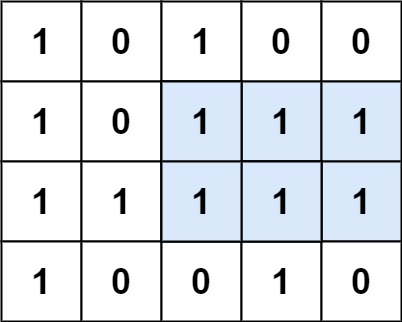
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：6
解释：最大矩形如上图所示。

示例 2：

输入：matrix = [["0"]]
输出：0

解题思路

思路 1：动态规划 + 单调栈

核心思想：将二维矩阵问题转化为一维直方图问题，然后使用单调栈求解最大矩形面积。

算法步骤：

构建高度数组：对于矩阵的每一行，计算以该行为底部的连续1的高度
转化为直方图问题：每一行的高度数组就相当于一个直方图
使用单调栈求解：对每个直方图使用单调栈算法求解最大矩形面积
更新全局最大值：记录所有行中的最大矩形面积

关键点：

对于每一行，如果当前元素是 '1'，则高度 $+1$ ；如果是 '0'，则高度重置为 $0$ 。
使用单调栈维护递增的高度序列，当遇到较小高度时，计算之前所有较大高度能形成的最大矩形。
在高度数组末尾添加 $0$ ，确保所有高度都能被处理。

思路 1：代码

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        # 在高度数组末尾添加 0，确保所有高度都能被处理
        heights.append(0)
        ans = 0
        stack = []  # 单调栈，存储高度数组的索引
        
        for i in range(len(heights)):
            # 当栈不为空且当前高度小于等于栈顶高度时
            while stack and heights[stack[-1]] >= heights[i]:
                # 弹出栈顶元素，计算以该高度为矩形高度的最大面积
                cur = stack.pop()
                # 计算矩形的左边界：栈中下一个元素的索引+1，如果栈为空则为 0
                left = stack[-1] + 1 if stack else 0
                # 计算矩形的右边界：当前索引 -1
                right = i - 1
                # 计算矩形面积：宽度 × 高度
                ans = max(ans, (right - left + 1) * heights[cur])
            # 将当前索引压入栈中
            stack.append(i)
        return ans

    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        # 处理空矩阵的情况
        if not matrix or not matrix[0]:
            return 0
            
        rows, cols = len(matrix), len(matrix[0])
        # 高度数组，记录以当前行为底部的连续 1 的高度
        heights = [0] * cols
        max_area = 0
        
        # 遍历矩阵的每一行
        for row in range(rows):
            # 更新高度数组
            for col in range(cols):
                if matrix[row][col] == '1':
                    # 如果当前元素是 '1'，高度 +1
                    heights[col] += 1
                else:
                    # 如果当前元素是 '0'，高度重置为 0
                    heights[col] = 0
            
            # 对当前行的高度数组使用单调栈算法计算最大矩形面积
            max_area = max(max_area, self.largestRectangleArea(heights[:]))
        
        return max_area

思路 1：复杂度分析

时间复杂度： $O(m \times n)$ ，其中 $m$ 是矩阵的行数， $n$ 是矩阵的列数。需要遍历矩阵的每个元素，对每一行使用单调栈的时间复杂度是 $O(n)$ 。
空间复杂度： $O(n)$ ，其中 $n$ 是矩阵的列数。需要维护高度数组和单调栈，空间复杂度为 $O(n)$ 。