---

0296. 最佳的碰头地点

• 标签：数组、数学、矩阵、排序
• 难度：困难

题目链接

• 0296. 最佳的碰头地点 - 力扣

题目大意

描述：

给定一个 $m \times n$ 的二进制网格 $grid$，其中 $1$ 表示某个朋友的家所处的位置。

要求：

返回「最小的」总行走距离。

说明：

• 总行走距离：指的是朋友们家到碰头地点的距离之和。使用「曼哈顿距离」来计算，其中 $distance(p1, p2) = |p2.x - p1.x| + |p2.y - p1.y|$。
• $m == grid.length$。
• $n == grid[i].length$。
• $1 \le m, n \le 200$。
• $grid[i][j]$ 等于 $0$ 或者 $1$。
• $grid$ 中 至少 有两个朋友。

示例：

• 示例 1：

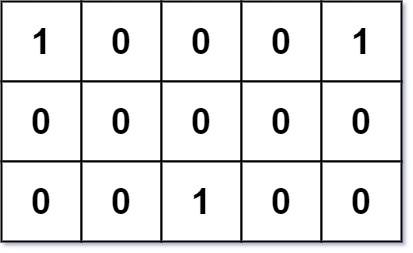
输入: grid = [[1,0,0,0,1],[0,0,0,0,0],[0,0,1,0,0]]
输出: 6 
解释: 给定的三个人分别住在(0,0)，(0,4) 和 (2,2):
     (0,2) 是一个最佳的碰面点，其总行走距离为 2 + 2 + 2 = 6，最小，因此返回 6。

• 示例 2：

输入: grid = [[1,1]]
输出: 1

解题思路

思路 1：中位数优化

这是一个经典的数学优化问题。关键观察是：对于曼哈顿距离，$x$ 坐标和 $y$ 坐标可以独立优化。

具体思路：

1. 收集所有朋友的位置坐标，分别得到 $x$ 坐标数组 $X$ 和 $y$ 坐标数组 $Y$
2. 对 $x$ 坐标和 $y$ 坐标分别排序
3. 最优的碰头地点的 $x$ 坐标是 $X$ 的中位数，$y$ 坐标是 $Y$ 的中位数
4. 计算所有朋友到最优碰头地点的曼哈顿距离之和

数学原理：对于一维情况，中位数是最小化绝对偏差和的最优解。由于曼哈顿距离可以分解为 $x$ 坐标差和 $y$ 坐标差的和，所以可以分别优化。

思路 1：代码

class Solution:
    def minTotalDistance(self, grid: List[List[int]]) -> int:
        """
        找到最佳的碰头地点，使所有朋友的总行走距离最小
        """
        m, n = len(grid), len(grid[0])
        
        # 收集所有朋友的位置坐标
        x_coords = []
        y_coords = []
        
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    x_coords.append(i)  # 行坐标
                    y_coords.append(j)  # 列坐标
        
        # 对坐标进行排序
        x_coords.sort()
        y_coords.sort()
        
        # 计算中位数位置
        k = len(x_coords)
        median_x = x_coords[k // 2]  # x 坐标的中位数
        median_y = y_coords[k // 2]  # y 坐标的中位数
        
        # 计算总距离
        total_distance = 0
        for i in range(k):
            total_distance += abs(x_coords[i] - median_x) + abs(y_coords[i] - median_y)
        
        return total_distance

思路 1：复杂度分析

• 时间复杂度：$O(m \times n + k \log k)$，其中 $m \times n$ 是遍历网格的时间，$k$ 是朋友的数量，$k \log k$ 是排序的时间。
• 空间复杂度：$O(k)$，用于存储所有朋友的坐标。