---

0298. 二叉树最长连续序列

• 标签：树、深度优先搜索、二叉树
• 难度：中等

题目链接

• 0298. 二叉树最长连续序列 - 力扣

题目大意

描述：

给你一棵指定的二叉树的根节点 $root$。

要求：

计算其中「最长连续序列路径」的长度。

说明：

• 「最长连续序列路径」是依次递增 $1$ 的路径。该路径，可以是从某个初始节点到树中任意节点，通过「父 - 子」关系连接而产生的任意路径。且必须从父节点到子节点，反过来是不可以的。
• 树中节点的数目在范围 $[1, 3 \times 10^{4}]$ 内。
• $-3 \times 10^{4} \le Node.val \le 3 \times 10^{4}$。

示例：

• 示例 1：

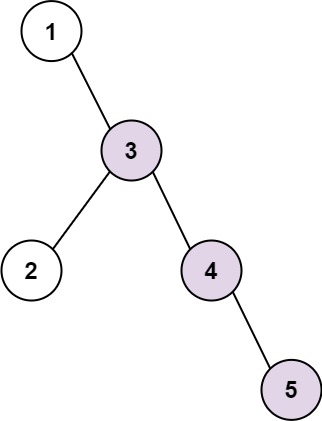
输入：root = [1,null,3,2,4,null,null,null,5]
输出：3
解释：当中，最长连续序列是 3-4-5 ，所以返回结果为 3。

• 示例 2：

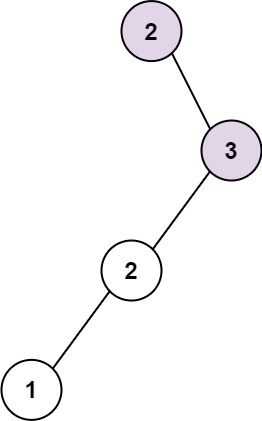
输入：root = [2,null,3,2,null,1]
输出：2
解释：当中，最长连续序列是 2-3 。注意，不是 3-2-1，所以返回 2。

解题思路

思路 1：深度优先搜索

这是一个典型的树形动态规划问题。我们需要找到二叉树中最长的连续递增序列路径。

我们可以使用深度优先搜索来解决这个问题：

1. 明确问题：对于每个节点，我们需要计算以该节点为起点的最长连续序列长度。
2. 状态定义：定义 $dfs(node)$ 函数，返回以 $node$ 为起点的最长连续序列长度。
3. 状态转移：
   • 如果 $node.left$ 存在且 $node.left.val = node.val + 1$，则左子树可以延续当前序列。
   • 如果 $node.right$ 存在且 $node.right.val = node.val + 1$，则右子树可以延续当前序列。
   • 取左右子树中的最大值，加上当前节点（长度为 $1$）。
4. 全局最优：在遍历过程中，维护全局最长序列长度 $max\_length$。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def longestConsecutive(self, root: Optional[TreeNode]) -> int:
        self.max_length = 0  # 全局最长序列长度
        
        def dfs(node):
            if not node:
                return 0
            
            # 计算以当前节点为起点的最长连续序列长度
            current_length = 1
            
            # 递归计算左右子树
            left_length = dfs(node.left)
            right_length = dfs(node.right)
            
            # 如果左子节点可以延续当前序列
            if node.left and node.left.val == node.val + 1:
                current_length = max(current_length, left_length + 1)
            
            # 如果右子节点可以延续当前序列
            if node.right and node.right.val == node.val + 1:
                current_length = max(current_length, right_length + 1)
            
            # 更新全局最长序列长度
            self.max_length = max(self.max_length, current_length)
            
            return current_length
        
        dfs(root)  # 从根节点开始深度优先搜索
        return self.max_length

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是树中节点的数量。每个节点都会被访问一次。
• 空间复杂度：$O(h)$，其中 $h$ 是树的高度。递归调用栈的深度最多为树的高度。