0261. 以图判树

ITCharge大约 3 分钟

---

0261. 以图判树

标签：深度优先搜索、广度优先搜索、并查集、图
难度：中等

题目链接

0261. 以图判树 - 力扣

题目大意

描述：

给定编号从 $0$ 到 $n - 1$ 的 $n$ 个结点。给定一个整数 $n$ 和一个 $edges$ 列表，其中 $edges[i] = [ai, bi]$ 表示图中节点 $ai$ 和 $bi$ 之间存在一条无向边。

要求：

如果这些边能够形成一个合法有效的树结构，则返回 $true$ ，否则返回 $false$ 。

说明：

$1 \le n \le 2000$ 。
$0 \le edges.length \le 5000$ 。
$edges[i].length == 2$ 。
$0 \le ai, bi \lt n$ 。
$ai \ne bi$ 。
不存在自循环或重复的边。

示例：

示例 1：

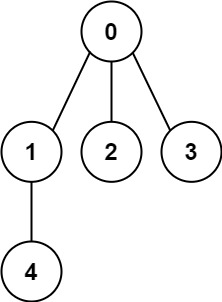
输入: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
输出: true

示例 2：

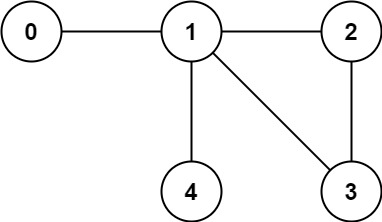
输入: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
输出: false

解题思路

思路 1：并查集

这是一个图论问题，需要判断给定的边是否能构成一棵有效的树。根据树的定义，一个有效的树必须满足以下条件：

连通性：所有 $n$ 个节点都连通。
无环性：图中不存在环。
边数条件：恰好有 $n - 1$ 条边。

我们可以使用并查集来解决这个问题。核心思想是：

如果边的数量不等于 $n-1$ ，则不可能构成树
使用并查集检测环：如果在添加边的过程中发现两个节点已经在同一个连通分量中，则存在环
最后检查是否所有节点都在同一个连通分量中

具体算法步骤：

检查边的数量：如果 $|edges| \neq n-1$ ，返回 $false$ 。
初始化并查集，每个节点的父节点为自己。
遍历每条边 $[a, b]$ $[a, b]$ ：
- 找到 $a$ 和 $b$ 的根节点 $root_a$ 和 $root_b$ 。
- 如果 $root_a = root_b$ ，说明存在环，返回 $false$ 。
- 否则将 $a$ 和 $b$ 合并到同一个连通分量。
检查连通性：所有节点是否都在同一个连通分量中。

思路 1：代码

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        # 如果边的数量不等于 n-1，则不可能构成树
        if len(edges) != n - 1:
            return False
        
        # 初始化并查集，每个节点的父节点为自己
        parent = list(range(n))
        
        def find(x):
            # 路径压缩优化
            if parent[x] != x:
                parent[x] = find(parent[x])
            return parent[x]
        
        def union(x, y):
            # 找到两个节点的根节点
            root_x, root_y = find(x), find(y)
            # 如果已经在同一个连通分量中，说明存在环
            if root_x == root_y:
                return False
            # 合并两个连通分量
            parent[root_x] = root_y
            return True
        
        # 遍历每条边，检查是否存在环
        for a, b in edges:
            if not union(a, b):
                return False
        
        # 检查连通性：所有节点是否都在同一个连通分量中
        root = find(0)
        for i in range(1, n):
            if find(i) != root:
                return False
        
        return True

思路 1：复杂度分析

时间复杂度： $O(n \times \alpha(n))$ ，其中 $\alpha(n)$ 是反阿克曼函数，在实际应用中可以认为是常数。遍历所有边需要 $O(n)$ 时间，每次并查集操作需要 $O(\alpha(n))$ 时间。
空间复杂度： $O(n)$ ，用于存储并查集的父节点数组。