---

0276. 栅栏涂色

• 标签：动态规划
• 难度：中等

题目链接

• 0276. 栅栏涂色 - 力扣

题目大意

描述：

有 $k$ 种颜色的涂料和一个包含 $n$ 个栅栏柱的栅栏，请你按下述规则为栅栏设计涂色方案：

• 每个栅栏柱可以用其中「一种」颜色进行上色。
• 相邻的栅栏柱「最多连续两个」颜色相同。

给定两个整数 $k$ 和 $n$。

要求：

返回所有有效的涂色「方案数」。

说明：

• $1 \le n \le 50$。
• $1 \le k \le 10^{5}$。
• 题目数据保证：对于输入的 $n$ 和 $k$，其答案在范围 $[0, 2^{31} - 1]$ 内。

示例：

• 示例 1：

输入：n = 3, k = 2
输出：6
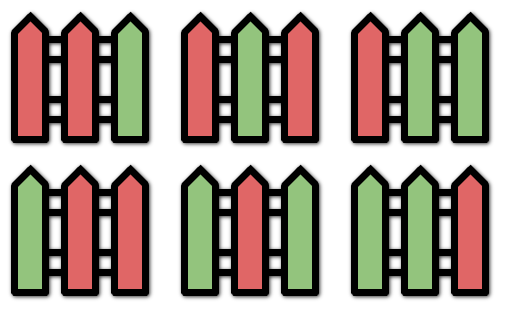
解释：所有的可能涂色方案如上图所示。注意，全涂红或者全涂绿的方案属于无效方案，因为相邻的栅栏柱 最多连续两个 颜色相同。

• 示例 2：

输入：n = 1, k = 1
输出：1

解题思路

思路 1：动态规划

这是一个经典的动态规划问题。我们需要计算在相邻栅栏柱最多连续两个颜色相同的约束下，有多少种涂色方案。

核心思想是：

• 定义状态：$dp[i]$ 表示前 $i$ 个栅栏柱的涂色方案数。
• 状态转移：考虑第 $i$ 个栅栏柱的涂色情况：
  • 如果第 $i$ 个栅栏柱与第 $i-1$ 个栅栏柱颜色不同，有 $dp[i-1] \times (k-1)$ 种方案。
  • 如果第 $i$ 个栅栏柱与第 $i-1$ 个栅栏柱颜色相同，但第 $i-1$ 个与第 $i-2$ 个颜色不同，有 $dp[i-2] \times (k-1)$ 种方案。
• 状态转移方程：$dp[i] = dp[i-1] \times (k-1) + dp[i-2] \times (k-1) = (dp[i-1] + dp[i-2]) \times (k-1)$

具体算法步骤：

1. 处理边界情况：如果 $n = 0$，返回 $0$；如果 $n = 1$，返回 $k$；如果 $n = 2$，返回 $k \times k$。
2. 初始化状态：$dp[0] = 0$，$dp[1] = k$，$dp[2] = k \times k$。
3. 状态转移：对于 $i$ 从 $3$ 到 $n$，计算 $dp[i] = (dp[i-1] + dp[i-2]) \times (k-1)$。
4. 返回 $dp[n]$。

思路 1：代码

class Solution:
    def numWays(self, n: int, k: int) -> int:
        # 处理边界情况
        if n == 0:
            return 0
        if n == 1:
            return k
        if n == 2:
            return k * k
        
        # 初始化 dp 数组
        # dp[i] 表示前 i 个栅栏柱的涂色方案数
        dp = [0] * (n + 1)
        dp[0] = 0
        dp[1] = k
        dp[2] = k * k
        
        # 状态转移
        for i in range(3, n + 1):
            # 第 i 个栅栏柱的涂色方案数 = (前 i-1 个的方案数 + 前 i-2 个的方案数) × (k-1)
            # 其中 k-1 表示与前面栅栏柱颜色不同的选择数
            dp[i] = (dp[i-1] + dp[i-2]) * (k - 1)
        
        return dp[n]

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是栅栏柱数量。需要遍历 $n$ 个状态进行状态转移。
• 空间复杂度：$O(n)$，需要 $O(n)$ 的空间存储 $dp$ 数组。