0361. 轰炸敌人

ITCharge大约 4 分钟

---

0361. 轰炸敌人

标签：数组、动态规划、矩阵
难度：中等

题目链接

0361. 轰炸敌人 - 力扣

题目大意

描述：

给定一个大小为 $m \times n$ 的矩阵 $grid$ ，其中每个单元格都放置有一个字符：

'W' 表示一堵墙。
'E' 表示一个敌人。
'0'（数字 $0$ ）表示一个空位。

要求：

返回你使用「一颗炸弹」可以击杀的最大敌人数目。

说明：

你只能把炸弹放在一个空位里。
由于炸弹的威力不足以穿透墙体，炸弹只能击杀同一行和同一列没被墙体挡住的敌人。
$m == grid.length$ 。
$n == grid[i].length$ 。
$1 \le m, n \le 500$ 。
$grid[i][j]$ 可以是 'W'、'E' 或 '0'。

示例：

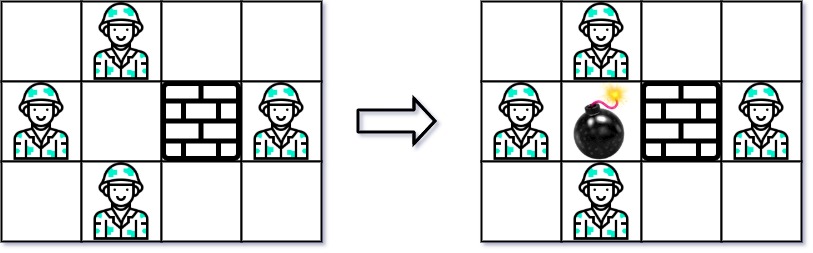
示例 1：

输入：grid = [["0","E","0","0"],["E","0","W","E"],["0","E","0","0"]]
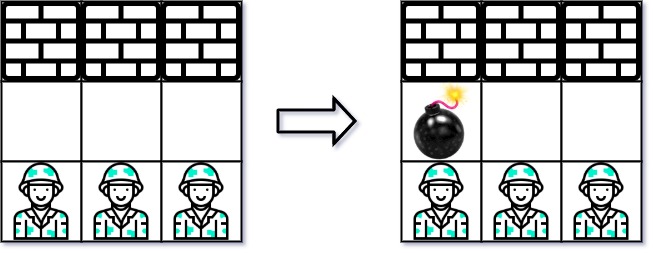
输出：3

示例 2：

输入：grid = [["W","W","W"],["0","0","0"],["E","E","E"]]
输出：1

解题思路

思路 1：动态规划 + 预处理

轰炸敌人问题可以通过动态规划预处理来解决。我们需要预先计算每个位置在四个方向上能击杀的敌人数，然后找到最大值。

问题分析：

对于矩阵 $grid$ 中的每个空位 $(i, j)$ ，炸弹可以击杀：

同一行中左右方向的敌人（被墙阻挡前）。
同一列中上下方向的敌人（被墙阻挡前）。

算法步骤：

预处理行方向：对每一行，从左到右和从右到左分别计算每个位置能击杀的敌人数。
预处理列方向：对每一列，从上到下和从下到上分别计算每个位置能击杀的敌人数。
计算最大值：遍历所有空位，计算四个方向击杀敌人数之和的最大值。

关键变量：

$m$ ：矩阵的行数。
$n$ ：矩阵的列数。
$row\_kills[i][j]$ ：位置 $(i, j)$ 在行方向上能击杀的敌人数。
$col\_kills[i][j]$ ：位置 $(i, j)$ 在列方向上能击杀的敌人数。
$max\_kills$ ：能击杀的最大敌人数。

思路 1：代码

class Solution:
    def maxKilledEnemies(self, grid: List[List[str]]) -> int:
        if not grid or not grid[0]:
            return 0
        
        m, n = len(grid), len(grid[0])
        max_kills = 0
        
        # 预处理：计算每个位置在行方向上能击杀的敌人数
        row_kills = [[0] * n for _ in range(m)]
        
        # 从左到右计算行方向的击杀数
        for i in range(m):
            count = 0
            for j in range(n):
                if grid[i][j] == 'W':
                    count = 0  # 遇到墙，重置计数
                elif grid[i][j] == 'E':
                    count += 1  # 遇到敌人，增加计数
                else:  # 空位
                    row_kills[i][j] += count
        
        # 从右到左计算行方向的击杀数
        for i in range(m):
            count = 0
            for j in range(n - 1, -1, -1):
                if grid[i][j] == 'W':
                    count = 0  # 遇到墙，重置计数
                elif grid[i][j] == 'E':
                    count += 1  # 遇到敌人，增加计数
                else:  # 空位
                    row_kills[i][j] += count
        
        # 预处理：计算每个位置在列方向上能击杀的敌人数
        col_kills = [[0] * n for _ in range(m)]
        
        # 从上到下计算列方向的击杀数
        for j in range(n):
            count = 0
            for i in range(m):
                if grid[i][j] == 'W':
                    count = 0  # 遇到墙，重置计数
                elif grid[i][j] == 'E':
                    count += 1  # 遇到敌人，增加计数
                else:  # 空位
                    col_kills[i][j] += count
        
        # 从下到上计算列方向的击杀数
        for j in range(n):
            count = 0
            for i in range(m - 1, -1, -1):
                if grid[i][j] == 'W':
                    count = 0  # 遇到墙，重置计数
                elif grid[i][j] == 'E':
                    count += 1  # 遇到敌人，增加计数
                else:  # 空位
                    col_kills[i][j] += count
        
        # 计算每个空位能击杀的敌人数，并更新最大值
        for i in range(m):
            for j in range(n):
                if grid[i][j] == '0':  # 空位
                    total_kills = row_kills[i][j] + col_kills[i][j]
                    max_kills = max(max_kills, total_kills)
        
        return max_kills

思路 1：复杂度分析

时间复杂度： $O(m \times n)$ ，其中 $m$ 是矩阵的行数， $n$ 是矩阵的列数。我们需要遍历矩阵四次（行方向两次，列方向两次），每次遍历的时间复杂度都是 $O(m \times n)$ 。
空间复杂度： $O(m \times n)$ ，需要两个 $m \times n$ 的二维数组来存储预处理结果。