---

0366. 寻找二叉树的叶子节点

• 标签：树、深度优先搜索、二叉树
• 难度：中等

题目链接

• 0366. 寻找二叉树的叶子节点 - 力扣

题目大意

描述：

给定一棵二叉树的 $root$ 节点。

要求：

请按照以下方式收集树的节点：

• 收集所有的叶子节点。
• 移除所有的叶子节点。
• 重复以上步骤，直到树为空。

说明：

• 树中节点的数量在 $[1, 10^{3}]$ 范围内。
• $-10^{3} \le Node.val \le 10^{3}$。

示例：

• 示例 1：

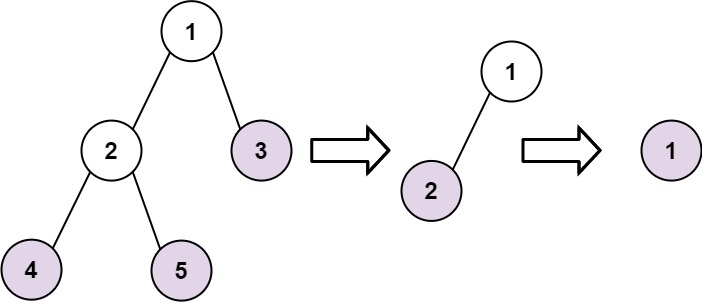
输入：root = [1,2,3,4,5]
输出：[[4,5,3],[2],[1]]
解释：
[[3,5,4],[2],[1]] 和 [[3,4,5],[2],[1]] 也被视作正确答案，因为每一层返回元素的顺序不影响结果。

• 示例 2：

输入：root = [1]
输出：[[1]]

解题思路

思路 1：深度优先搜索 + 高度计算

这道题的核心思想是：根据节点的高度来分组收集叶子节点。

解题步骤：

1. 定义节点高度：设节点 $node$ 的高度为 $height(node)$，表示从该节点到叶子节点的最长路径上的边数。
   • 叶子节点的高度为 $0$。
   • 非叶子节点的高度为其左右子树高度的最大值加 $1$。
2. 递归计算高度：使用深度优先搜索遍历二叉树，计算每个节点的高度。
3. 按高度分组：将具有相同高度的节点值收集到同一个列表中。
4. 返回结果：按照高度从 $0$ 到最大高度的顺序返回结果列表。

关键点：

• 第一次收集的叶子节点高度为 $0$。
• 移除叶子节点后，新的叶子节点高度为 $1$。
• 以此类推，第 $i$ 轮收集的节点高度为 $i-1$。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def findLeaves(self, root: Optional[TreeNode]) -> List[List[int]]:
        def getHeight(node):
            """计算节点高度并收集节点值"""
            if not node:
                return -1  # 空节点高度为-1
            
            # 递归计算左右子树的高度
            left_height = getHeight(node.left)
            right_height = getHeight(node.right)
            
            # 当前节点的高度 = max(左子树高度, 右子树高度) + 1
            current_height = max(left_height, right_height) + 1
            
            # 确保结果列表有足够的长度
            while len(result) <= current_height:
                result.append([])
            
            # 将当前节点值添加到对应高度的列表中
            result[current_height].append(node.val)
            
            return current_height
        
        result = []
        getHeight(root)
        return result

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是树中节点的数量。每个节点被访问一次。
• 空间复杂度：$O(n)$，其中 $n$ 是树中节点的数量。递归调用栈的深度最多为树的高度，最坏情况下为 $O(n)$；结果列表最多存储 $n$ 个节点值。