0388. 文件的最长绝对路径

ITCharge大约 4 分钟

---

0388. 文件的最长绝对路径

标签：栈、深度优先搜索、字符串
难度：中等

题目链接

0388. 文件的最长绝对路径 - 力扣

题目大意

描述：

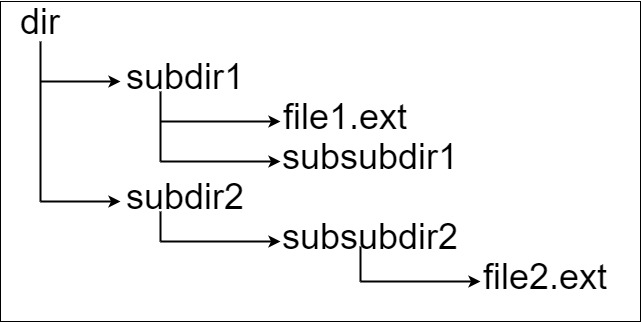
假设有一个同时存储文件和目录的文件系统。下图展示了文件系统的一个示例：

这里将 $dir$ 作为根目录中的唯一目录。 $dir$ 包含两个子目录 $subdir1$ 和 $subdir2$ 。

$subdir1$ 包含文件 $file1.ext$ 和子目录 $subsubdir1$ ；
$subdir2$ 包含子目录 $subsubdir2$ ，该子目录下包含文件 $file2.ext$ 。

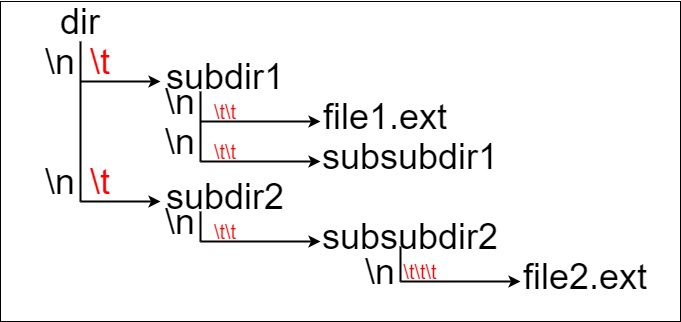
在文本格式中，如下所示(⟶表示制表符)：

dir
⟶ $subdir1$
⟶ ⟶ $file1$.ext
⟶ ⟶ $subsubdir1$
⟶ $subdir2$
⟶ ⟶ $subsubdir2$
⟶ ⟶ ⟶ $file2$.ext

如果是代码表示，上面的文件系统可以写为 "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext"。'\n' 和 '\t' 分别是换行符和制表符。

文件系统中的每个文件和文件夹都有一个唯一的「绝对路径」，即必须打开才能到达文件/目录所在位置的目录顺序，所有路径用 '/' 连接。

上面例子中，指向 $file2.ext$ 的「绝对路径」是 "dir/subdir2/subsubdir2/file2.ext"。每个目录名由字母、数字和/或空格组成，每个文件名遵循 $name.extension$ 的格式，其中 $name$ 和 $extension$ 由字母、数字和 / 或空格组成。

给定一个以上述格式表示文件系统的字符串 $input$ 。

要求：

返回文件系统中指向「文件」的「最长绝对路径」的长度。如果系统中没有文件，返回 $0$ 。

说明：

$1 \le input.length \le 10^{4}$ 。
$input$ 可能包含小写或大写的英文字母，一个换行符 '\n'，一个制表符 '\t'，一个点 '.'，一个空格 ' '，和数字。

示例：

示例 1：

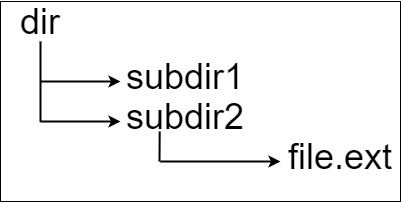
输入：input = "dir\n\tsubdir1\n\tsubdir2\n\t\tfile.ext"
输出：20
解释：只有一个文件，绝对路径为 "dir/subdir2/file.ext" ，路径长度 20

示例 2：

输入：input = "dir\n\tsubdir1\n\t\tfile1.ext\n\t\tsubsubdir1\n\tsubdir2\n\t\tsubsubdir2\n\t\t\tfile2.ext"
输出：32
解释：存在两个文件：
"dir/subdir1/file1.ext" ，路径长度 21
"dir/subdir2/subsubdir2/file2.ext" ，路径长度 32
返回 32 ，因为这是最长的路径

解题思路

思路 1：栈模拟

这道题的核心思想是：使用栈来模拟文件系统的层级结构，通过制表符数量判断层级深度，计算每个文件的绝对路径长度。

解题步骤：

分割输入：将输入字符串按换行符 \n 分割成每一行。
栈维护路径：
- 使用栈 $stack$ 维护当前路径的各个层级。
- 栈中存储每个层级对应的路径长度。
- 栈顶元素表示当前层级的路径长度。
层级判断：
- 通过计算每行开头的制表符 \t 数量来确定层级深度 $depth$ 。
- 制表符数量即为层级深度。
路径计算：
- 如果当前层级 $depth$ 小于栈的长度，说明需要回退到对应层级。
- 弹出栈中深度大于等于 $depth$ 的所有元素。
- 将当前行（去除制表符）的长度加入栈中。
- 如果当前行是文件（包含 .），则计算完整路径长度并更新最大值。
路径长度计算：
- 完整路径长度 = 栈中所有元素之和 + 栈的长度 - 1（分隔符 / 的数量）
- 即： $total\_length = \sum_{i=0}^{stack.size-1} stack[i] + (stack.size - 1)$

关键点：

栈的大小表示当前路径的层级深度。
栈中每个元素表示对应层级文件 / 目录名的长度。
只有文件（包含 .）才参与最长路径的计算。
路径分隔符 / 的数量等于层级数减 $1$ 。

思路 1：代码

class Solution:
    def lengthLongestPath(self, input: str) -> int:
        # 按换行符分割输入字符串
        lines = input.split('\n')
        # 使用栈维护当前路径的各个层级长度
        stack = []
        # 记录最长文件路径长度
        max_length = 0
        
        for line in lines:
            # 计算当前行的层级深度（制表符数量）
            depth = 0
            while depth < len(line) and line[depth] == '\t':
                depth += 1
            
            # 获取当前行去除制表符后的内容
            name = line[depth:]
            
            # 如果当前层级小于栈的大小，需要回退到对应层级
            while len(stack) > depth:
                stack.pop()
            
            # 将当前行长度加入栈中
            stack.append(len(name))
            
            # 如果当前行是文件（包含 '.'），计算完整路径长度
            if '.' in name:
                # 完整路径长度 = 所有层级长度之和 + 分隔符数量
                total_length = sum(stack) + len(stack) - 1
                max_length = max(max_length, total_length)
        
        return max_length

思路 1：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 是输入字符串的长度。需要遍历所有行，每行最多入栈和出栈一次。
空间复杂度： $O(d)$ ，其中 $d$ 是文件系统的最大深度。栈的最大深度不会超过文件系统的层级深度。