0363. 矩形区域不超过 K 的最大数值和

ITCharge大约 4 分钟

---

0363. 矩形区域不超过 K 的最大数值和

标签：数组、二分查找、矩阵、有序集合、前缀和
难度：困难

题目链接

0363. 矩形区域不超过 K 的最大数值和 - 力扣

题目大意

描述：

给定一个 $m \times n$ 的矩阵 $matrix$ 和一个整数 $k$ 。

要求：

找出并返回矩阵内部矩形区域的不超过 $k$ 的最大数值和。

题目数据保证总会存在一个数值和不超过 $k$ 的矩形区域。

说明：

$m == matrix.length$ 。
$n == matrix[i].length$ 。
$1 \le m, n \le 10^{3}$ 。
$-10^{3} \le matrix[i][j] \le 10^{3}$ 。
$-10^{5} \le k \le 10^{5}$ 。
进阶：如果行数远大于列数，该如何设计解决方案？

示例：

示例 1：

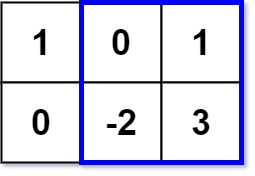
输入：matrix = [[1,0,1],[0,-2,3]], k = 2
输出：2
解释：蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。

示例 2：

输入：matrix = [[2,2,-1]], k = 3
输出：3

解题思路

思路 1：前缀和 + 有序集合

这道题的核心思想是：将二维问题转化为一维问题，使用前缀和配合有序集合来快速查找不超过 $k$ 的最大子数组和。

解题步骤：

枚举列边界：固定矩形的左右边界 $left$ 和 $right$ ，将二维问题转化为一维问题。
计算行前缀和：对于每一行，计算从 $left$ 到 $right$ 的列和，得到一维数组 $row\_sums$ 。
前缀和优化：使用前缀和数组 $prefix\_sums$ ，其中 $prefix\_sums[i] = \sum_{j=0}^{i-1} row\_sums[j]$ 。
有序集合查找：对于每个位置 $i$ ，我们需要找到最大的 $j < i$ ，使得 $prefix\_sums[i] - prefix\_sums[j] \leq k$ ，即 $prefix\_sums[j] \geq prefix\_sums[i] - k$ 。
二分查找优化：使用有序集合（如 SortedList）存储已处理的前缀和，通过二分查找快速找到满足条件的最小前缀和。

关键点：

时间复杂度从 $O(m^2n^2)$ 优化到 $O(m^2n \log n)$ 。
使用有序集合维护前缀和的单调性，支持 $O(\log n)$ 的插入和查找操作。
对于每个固定的列边界，问题转化为"最大子数组和不超过 $k$ "的一维问题。

算法正确性：

设当前处理到位置 $i$ ，前缀和为 $prefix\_sums[i]$ ，我们需要找到最大的 $j < i$ 使得： $prefix\_sums[i] - prefix\_sums[j] \leq k$ 。

即： $prefix\_sums[j] \geq prefix\_sums[i] - k$ 。

由于我们要找最大的子数组和，所以应该找最小的满足条件的 $prefix\_sums[j]$ ，这样 $prefix\_sums[i] - prefix\_sums[j]$ 最大。

思路 1：代码

from sortedcontainers import SortedList
from typing import List

class Solution:
    def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int:
        m, n = len(matrix), len(matrix[0])
        result = float('-inf')
        
        # 枚举左边界
        for left in range(n):
            # 存储当前列边界下的行和
            row_sums = [0] * m
            
            # 枚举右边界
            for right in range(left, n):
                # 计算每行从left到right的列和
                for i in range(m):
                    row_sums[i] += matrix[i][right]
                
                # 使用有序集合维护前缀和
                sorted_list = SortedList([0])  # 初始化为0，表示空子数组
                prefix_sum = 0
                
                # 遍历每一行，计算前缀和
                for row_sum in row_sums:
                    prefix_sum += row_sum
                    
                    # 查找满足条件的最小前缀和
                    # 需要找到 prefix_sum - x <= k，即 x >= prefix_sum - k
                    target = prefix_sum - k
                    idx = sorted_list.bisect_left(target)
                    
                    # 如果找到了满足条件的前缀和
                    if idx < len(sorted_list):
                        current_sum = prefix_sum - sorted_list[idx]
                        result = max(result, current_sum)
                    
                    # 将当前前缀和加入有序集合
                    sorted_list.add(prefix_sum)
        
        return result

思路 1：复杂度分析

时间复杂度： $O(m^2n \log n)$ ，其中 $m$ 是矩阵的行数， $n$ 是矩阵的列数。外层双重循环枚举列边界的时间复杂度是 $O(n^2)$ ，内层对每行计算前缀和的时间复杂度是 $O(m)$ ，有序集合的插入和查找操作的时间复杂度是 $O(\log n)$ 。
空间复杂度： $O(m + n)$ ，其中 $m$ 是矩阵的行数， $n$ 是矩阵的列数。主要空间消耗来自行和数组 $row\_sums$ 和有序集合 $sorted\_list$ 。