0305. 岛屿数量 II

ITCharge大约 4 分钟

---

0305. 岛屿数量 II

标签：并查集、数组、哈希表
难度：困难

题目链接

0305. 岛屿数量 II - 力扣

题目大意

描述：

给定一个大小为 $m \times n$ 的二维二进制网格 $grid$ 。网格表示一个地图，其中， $0$ 表示水， $1$ 表示陆地。最初， $grid$ 中的所有单元格都是水单元格（即，所有单元格都是 $0$ ）。

可以通过执行 $addLand$ 操作，将某个位置的水转换成陆地。给你一个数组 $positions$ ，其中 $positions[i] = [ri, ci]$ 是要执行第 $i$ 次操作的位置 $(ri, ci)$ 。

要求：

返回一个整数数组 $answer$ ，其中 $answer[i]$ 是将单元格 $(ri, ci)$ 转换为陆地后，地图中岛屿的数量。

说明：

岛屿：指的是被「水」包围的「陆地」，通过水平方向或者垂直方向上相邻的陆地连接而成。你可以假设地图网格的四边均被无边无际的「水」所包围。
$1 \le m, n, positions.length \le 10^{4}$ 。
$1 \le m \times n \le 10^{4}$ 。
$positions[i].length == 2$ 。
$0 \le ri \lt m$ 。
$0 \le ci \lt n$ 。
进阶：你可以设计一个时间复杂度 $O(k \log(mn))$ 的算法解决此问题吗？（其中 $k == positions.length$ ）。

示例：

示例 1：

输入：m = 3, n = 3, positions = [[0,0],[0,1],[1,2],[2,1]]
输出：[1,1,2,3]
解释：
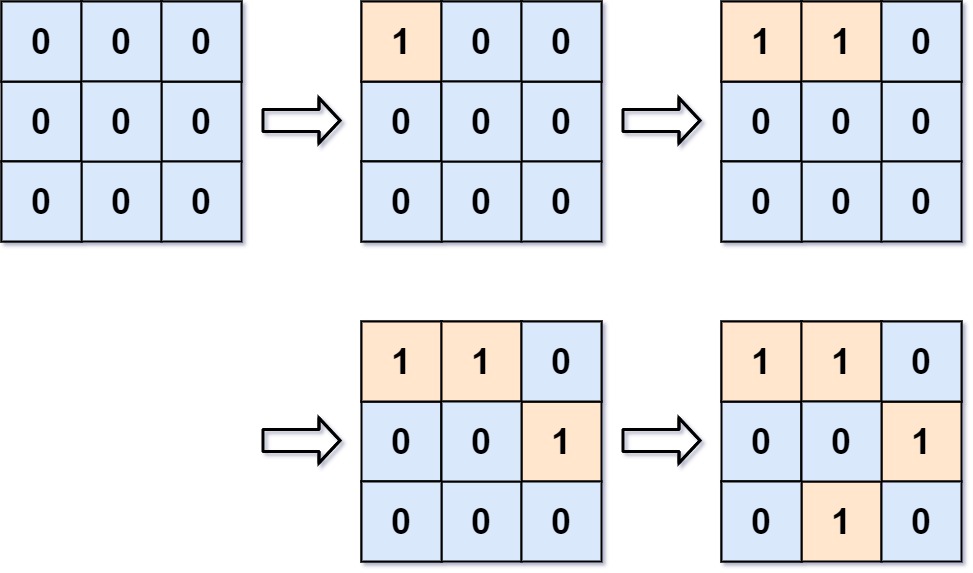
起初，二维网格 grid 被全部注入「水」。（0 代表「水」，1 代表「陆地」）
- 操作 #1：addLand(0, 0) 将 grid[0][0] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #2：addLand(0, 1) 将 grid[0][1] 的水变为陆地。此时存在 1 个岛屿。
- 操作 #3：addLand(1, 2) 将 grid[1][2] 的水变为陆地。此时存在 2 个岛屿。
- 操作 #4：addLand(2, 1) 将 grid[2][1] 的水变为陆地。此时存在 3 个岛屿。

示例 2：

输入：m = 1, n = 1, positions = [[0,0]]
输出：[1]

解题思路

思路 1：并查集

使用并查集（Union Find）数据结构来动态维护岛屿的连通性。每次添加一个新的陆地时，检查其四个方向（上、下、左、右）是否已有陆地，如果有则进行合并操作。

具体步骤：

初始化：创建并查集，大小为 $m \times n$ ，初始时所有位置都是水（不属于任何岛屿）。
添加陆地：对于每个位置 $(r_i, c_i)$ $(r_{i}, c_{i})$ ：
- 将位置 $(r_i, c_i)$ 标记为陆地。
- 检查四个方向 $(r_i-1, c_i)$ 、 $(r_i+1, c_i)$ 、 $(r_i, c_i-1)$ 、 $(r_i, c_i+1)$ 是否已有陆地。
- 如果有陆地，则与当前新添加的陆地合并到同一个连通分量中
- 统计当前连通分量的数量
坐标转换：将二维坐标 $(r, c)$ 转换为一维索引 $index = r \times n + c$ ，便于并查集操作。
岛屿计数：每次添加陆地后，统计并查集中独立连通分量的数量。

思路 1：代码

class UnionFind:
    def __init__(self, n):
        """初始化并查集"""
        self.parent = [i for i in range(n)]  # 父节点数组
        self.rank = [0] * n                  # 秩数组，用于路径压缩优化
        self.count = 0                       # 连通分量数量
    
    def find(self, x):
        """查找根节点，带路径压缩"""
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])  # 路径压缩
        return self.parent[x]
    
    def union(self, x, y):
        """合并两个节点"""
        root_x = self.find(x)
        root_y = self.find(y)
        
        if root_x == root_y:
            return False  # 已经在同一个连通分量中
        
        # 按秩合并
        if self.rank[root_x] < self.rank[root_y]:
            self.parent[root_x] = root_y
        elif self.rank[root_x] > self.rank[root_y]:
            self.parent[root_y] = root_x
        else:
            self.parent[root_y] = root_x
            self.rank[root_x] += 1
        
        self.count -= 1  # 合并后连通分量数量减 1
        return True
    
    def add_island(self, x):
        """添加一个新的岛屿"""
        if self.parent[x] != x:  # 已经是陆地
            return
        self.parent[x] = x
        self.count += 1  # 新增一个连通分量

class Solution:
    def numIslands2(self, m: int, n: int, positions: List[List[int]]) -> List[int]:
        """使用并查集解决岛屿数量 II 问题"""
        # 方向数组：上、下、左、右
        directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
        
        # 初始化并查集
        uf = UnionFind(m * n)
        
        # 标记哪些位置是陆地
        is_land = [False] * (m * n)
        
        result = []
        
        for r, c in positions:
            # 将二维坐标转换为一维索引
            index = r * n + c
            
            # 如果该位置已经是陆地，直接返回当前岛屿数量
            if is_land[index]:
                result.append(uf.count)
                continue
            
            # 标记为陆地
            is_land[index] = True
            uf.add_island(index)
            
            # 检查四个方向，合并相邻的陆地
            for dr, dc in directions:
                new_r, new_c = r + dr, c + dc
                
                # 检查边界
                if 0 <= new_r < m and 0 <= new_c < n:
                    new_index = new_r * n + new_c
                    
                    # 如果相邻位置是陆地，进行合并
                    if is_land[new_index]:
                        uf.union(index, new_index)
            
            # 记录当前岛屿数量
            result.append(uf.count)
        
        return result

思路 1：复杂度分析

时间复杂度： $O(k \times \alpha(mn))$ ，其中 $k$ 是 $positions$ 的长度， $\alpha$ 是反阿克曼函数，可以认为是常数。每次操作需要检查四个方向并进行并查集操作。
空间复杂度： $O(mn)$ ，用于存储并查集的父节点数组、秩数组和陆地标记数组。