0308. 二维区域和检索 - 矩阵可修改

ITCharge大约 3 分钟

---

0308. 二维区域和检索 - 矩阵可修改

标签：设计、树状数组、线段树、数组、矩阵
难度：中等

题目链接

0308. 二维区域和检索 - 矩阵可修改 - 力扣

题目大意

描述：

给定一个二维矩阵 $matrix$ 。

要求：

处理以下类型的多个查询:

更新 $matrix$ 中单元格的值。
计算由左上角 $(row1, col1)$ 和右下角 $(row2, col2)$ 定义的 $matrix$ 内矩阵元素的和。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 用整数矩阵 $matrix$ 初始化对象。
void update(int row, int col, int val) 更新 $matrix[row][col]$ 的值到 $val$ 。
int sumRegion(int row1, int col1, int row2, int col2) 返回矩阵 $matrix$ 中指定矩形区域元素的和，该区域由左上角 $(row1, col1)$ 和右下角 $(row2, col2)$ 界定。

说明：

$m == matrix.length$ 。
$n == matrix[i].length$ 。
$1 \le m, n \le 200$ 。
$-10^{3} \le matrix[i][j] \le 10^{3}$ 。
$0 \le row \lt m$ 。
$0 \le col \lt n$ 。
$-10^{3} \le val \le 10^{3}$ 。
$0 \le row1 \le row2 \lt m$ 。
$0 \le col1 \le col2 \lt n$ 。
最多调用 $5000$ 次 sumRegion 和 update 方法。

示例：

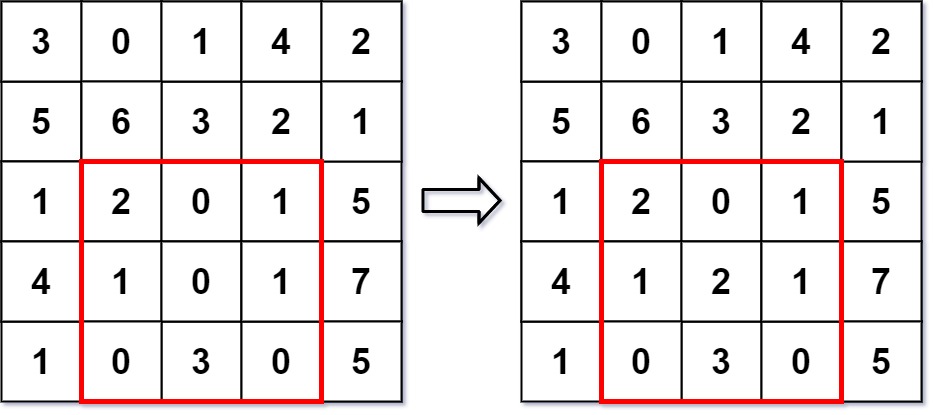
示例 1：

输入
["NumMatrix", "sumRegion", "update", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [3, 2, 2], [2, 1, 4, 3]]
输出
[null, 8, null, 10]

解释
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // 返回 8 (即, 左侧红色矩形的和)
numMatrix.update(3, 2, 2);       // 矩阵从左图变为右图
numMatrix.sumRegion(2, 1, 4, 3); // 返回 10 (即，右侧红色矩形的和)

解题思路

思路 1：二维前缀和数组

算法思路：

使用二维前缀和数组来快速计算矩形区域的和。二维前缀和数组 $prefix[i][j]$ 表示从 $(0, 0)$ 到 $(i-1, j-1)$ 的矩形区域内所有元素的和。

对于查询矩形区域 $(row1, col1)$ 到 $(row2, col2)$ 的和，可以使用容斥原理：

sum = prefix[row2+1][col2+1] - prefix[row1][col2+1] - prefix[row2+1][col1] + prefix[row1][col1]

具体实现：

初始化：
- 创建二维前缀和数组 $prefix$ ，大小为 $(m+1) \times (n+1)$ ，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。
- 计算前缀和： $prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1] + matrix[i-1][j-1]$
更新操作：
- 计算差值 $diff = val - matrix[row][col]$
- 更新原矩阵： $matrix[row][col] = val$
- 更新前缀和数组：从 $(row+1, col+1)$ 开始，所有受影响的区域都需要加上 $diff$
查询操作：
- 使用容斥原理计算指定矩形区域的和

思路 1：代码

from typing import List

class NumMatrix:
    def __init__(self, matrix: List[List[int]]):
        """初始化二维前缀和数组"""
        self.matrix = matrix
        self.m, self.n = len(matrix), len(matrix[0])
        
        # 创建前缀和数组，大小为 (m+1) x (n+1)
        self.prefix = [[0] * (self.n + 1) for _ in range(self.m + 1)]
        
        # 计算前缀和
        for i in range(1, self.m + 1):
            for j in range(1, self.n + 1):
                self.prefix[i][j] = (self.prefix[i-1][j] + 
                                   self.prefix[i][j-1] - 
                                   self.prefix[i-1][j-1] + 
                                   matrix[i-1][j-1])

    def update(self, row: int, col: int, val: int) -> None:
        """更新矩阵元素并维护前缀和数组"""
        # 计算差值
        diff = val - self.matrix[row][col]
        self.matrix[row][col] = val
        
        # 更新前缀和数组
        for i in range(row + 1, self.m + 1):
            for j in range(col + 1, self.n + 1):
                self.prefix[i][j] += diff

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        """使用容斥原理计算矩形区域和"""
        return (self.prefix[row2+1][col2+1] - 
                self.prefix[row1][col2+1] - 
                self.prefix[row2+1][col1] + 
                self.prefix[row1][col1])


# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# obj.update(row,col,val)
# param_2 = obj.sumRegion(row1,col1,row2,col2)

思路 1：复杂度分析

时间复杂度：
- 构造函数： $O(m \times n)$ ，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。需要计算整个前缀和数组。
- update 函数： $O(m \times n)$ ，最坏情况下需要更新整个前缀和数组。
- sumRegion 函数： $O(1)$ ，直接通过前缀和数组计算。
空间复杂度： $O(m \times n)$ ，需要存储前缀和数组。