---

0335. 路径交叉

• 标签：几何、数组、数学
• 难度：困难

题目链接

• 0335. 路径交叉 - 力扣

题目大意

描述：

给定一个整数数组 $distance$。

从 X-Y 平面上的点 $(0,0)$ 开始，先向北移动 $distance[0]$ 米，然后向西移动 $distance[1]$ 米，向南移动 $distance[2]$ 米，向东移动 $distance[3]$ 米，持续移动。也就是说，每次移动后你的方位会发生逆时针变化。

要求：

判断你所经过的路径是否相交。如果相交，返回 $true$；否则，返回 $false$。

说明：

• $1 \le distance.length \le 10^{5}$。
• $1 \le distance[i] \le 10^{5}$。

示例：

• 示例 1：

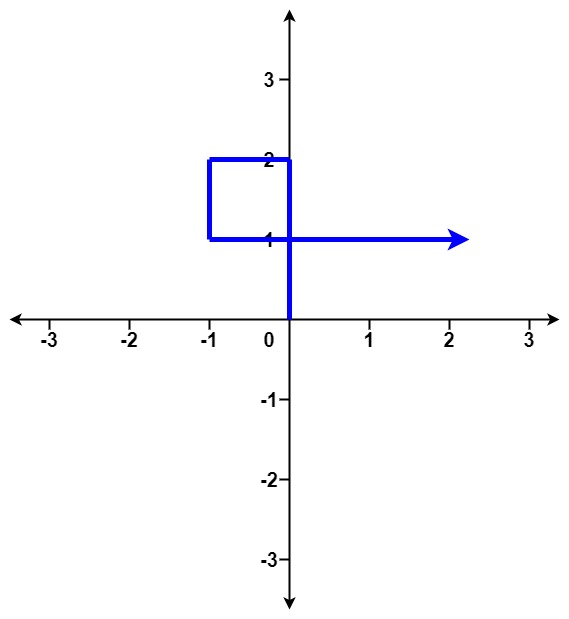
输入：distance = [2,1,1,2]
输出：true

• 示例 2：

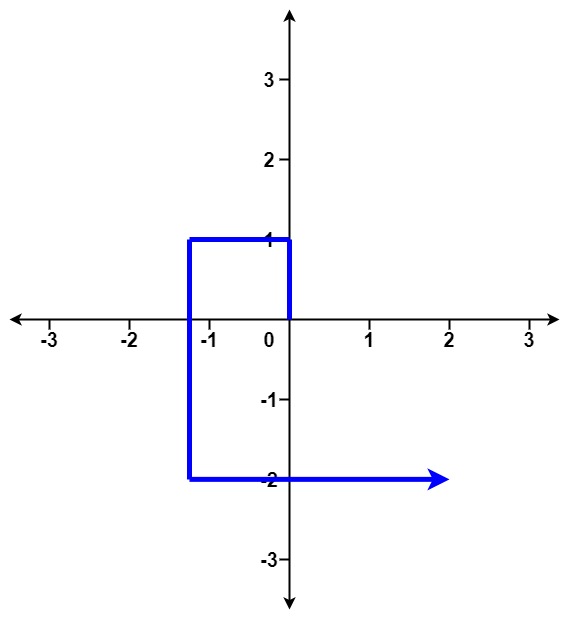
输入：distance = [1,2,3,4]
输出：false

解题思路

思路 1：分类讨论

路径交叉问题可以通过分析路径的几何特征来解决。关键在于：第 $i$ 条线段只可能与第 $i-3$、$i-4$、$i-5$ 条线段相交。

设路径移动序列为 $distance = [d_0, d_1, d_2, d_3, ...]$，从点 $(0, 0)$ 开始，按照北、西、南、东的方向依次循环移动。

路径交叉主要有以下三种情况：

1. 第 $i$ 条线段与第 $i-3$ 条线段相交：当 $i \ge 3$ 时，如果 $d_i \ge d_{i-2}$ 且 $d_{i-1} \le d_{i-3}$，则发生交叉。

2. 第 $i$ 条线段与第 $i-4$ 条线段相交：当 $i \ge 4$ 时，如果 $d_{i-1} = d_{i-3}$ 且 $d_i + d_{i-4} \ge d_{i-2}$，则发生交叉。

3. 第 $i$ 条线段与第 $i-5$ 条线段相交：当 $i \ge 5$ 时，需要满足多个条件才会交叉。

算法步骤：

1. 遍历路径数组，从第 4 条线段开始检查。
2. 对于每条线段，检查是否与前面的第 3、4、5 条线段相交。
3. 如果发现交叉，返回 $true$；否则继续检查。
4. 如果遍历完所有线段都没有交叉，返回 $false$。

思路 1：代码

class Solution:
    def isSelfCrossing(self, distance: List[int]) -> bool:
        n = len(distance)
        
        # 路径长度小于 4 时不可能交叉
        if n < 4:
            return False
        
        # 从第 4 条线段开始检查
        for i in range(3, n):
            # 第 i 条线段与第 i-3 条线段相交
            if i >= 3:
                if distance[i] >= distance[i - 2] and distance[i - 1] <= distance[i - 3]:
                    return True
            
            # 第 i 条线段与第 i-4 条线段相交
            if i >= 4:
                if distance[i - 1] == distance[i - 3] and distance[i] + distance[i - 4] >= distance[i - 2]:
                    return True
            
            # 第 i 条线段与第 i-5 条线段相交
            if i >= 5:
                if (distance[i - 2] >= distance[i - 4] and 
                    distance[i - 3] >= distance[i - 1] and 
                    distance[i - 1] + distance[i - 5] >= distance[i - 3] and 
                    distance[i] + distance[i - 4] >= distance[i - 2]):
                    return True
        
        return False

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是路径数组的长度。需要遍历数组一次，每个位置的处理时间是常数时间。
• 空间复杂度：$O(1)$，只使用了常数额外空间，没有使用额外的数据结构。