0317. 离建筑物最近的距离

ITCharge大约 3 分钟

---

0317. 离建筑物最近的距离

标签：广度优先搜索、数组、矩阵
难度：困难

题目链接

0317. 离建筑物最近的距离 - 力扣

题目大意

描述：
给定一个 $m \times n$ 的网格，值为 $0$ 、 $1$ 或 $2$ ，其中:

每一个 $0$ 代表一块你可以自由通过的「空地」。
每一个 $1$ 代表一个你不能通过的「建筑」。
每一个 $2$ 标记一个你不能通过的「障碍」。

你想要在一块空地上建造一所房子，在「最短的总旅行距离」内到达所有的建筑。你只能上下左右移动。

要求：

返回到该房子的「最短旅行距离」。如果根据上述规则无法建造这样的房子，则返回 $-1$ 。

说明：

总旅行距离：是朋友们家到聚会地点的距离之和。
$m == grid.length$ 。
$n == grid[i].length$ 。
$1 \le m, n \le 50$ 。
$grid[i][j]$ 是 $0$ , $1$ 或 $2$ 。
$grid$ 中至少有一幢建筑。

示例：

示例 1：

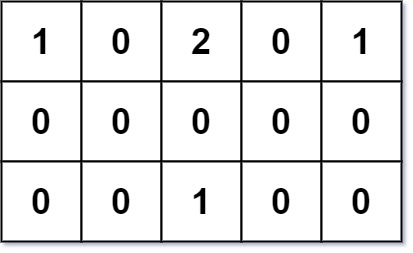
输入：grid = [[1,0,2,0,1],[0,0,0,0,0],[0,0,1,0,0]]
输出：7 
解析：给定三个建筑物 (0,0)、(0,4) 和 (2,2) 以及一个位于 (0,2) 的障碍物。
由于总距离之和 3+3+1=7 最优，所以位置 (1,2) 是符合要求的最优地点。
故返回 7。

示例 2：

输入: grid = [[1,0]]
输出: 1

解题思路

思路 1：多源 BFS

核心思想：从每个建筑物出发，使用 BFS 计算到所有空地的距离，然后找到距离所有建筑物总距离最小的空地。

算法步骤：

统计建筑物数量：遍历网格，统计建筑物（值为 $1$ ）的总数 $buildingCount$ 。
多源 BFS：对每个建筑物执行 BFS，计算到所有空地的距离：
- 使用队列 $queue$ 存储待访问的位置。
- 使用 $dist$ 数组记录从当前建筑物到各位置的距离。
- 使用 $reachCount$ 数组记录每个位置能到达的建筑物数量。
距离累加：使用 $totalDist$ 数组累加所有建筑物到各位置的距离。
寻找最优解：遍历所有空地，找到能到达所有建筑物且总距离最小的位置。

思路 1：代码

class Solution:
    def shortestDistance(self, grid: List[List[int]]) -> int:
        if not grid or not grid[0]:
            return -1
        
        m, n = len(grid), len(grid[0])
        # 统计建筑物数量
        building_count = 0
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:
                    building_count += 1
        
        # 记录每个位置能到达的建筑物数量和总距离
        reach_count = [[0] * n for _ in range(m)]
        total_dist = [[0] * n for _ in range(m)]
        
        # 方向数组：上下左右
        directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
        
        # 从每个建筑物开始 BFS
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1:  # 找到建筑物
                    # BFS 计算从当前建筑物到所有空地的距离
                    queue = [(i, j)]
                    dist = [[-1] * n for _ in range(m)]
                    dist[i][j] = 0
                    
                    while queue:
                        x, y = queue.pop(0)
                        # 遍历四个方向
                        for dx, dy in directions:
                            nx, ny = x + dx, y + dy
                            # 检查边界和是否为空地
                            if (0 <= nx < m and 0 <= ny < n and 
                                grid[nx][ny] == 0 and dist[nx][ny] == -1):
                                dist[nx][ny] = dist[x][y] + 1
                                queue.append((nx, ny))
                                # 累加距离和到达的建筑物数量
                                total_dist[nx][ny] += dist[nx][ny]
                                reach_count[nx][ny] += 1
        
        # 寻找能到达所有建筑物且总距离最小的空地
        min_dist = float('inf')
        for i in range(m):
            for j in range(n):
                if (grid[i][j] == 0 and 
                    reach_count[i][j] == building_count and 
                    total_dist[i][j] < min_dist):
                    min_dist = total_dist[i][j]
        
        return min_dist if min_dist != float('inf') else -1

思路 1：复杂度分析

时间复杂度： $O(m \times n \times k)$ ，其中 $m$ 和 $n$ 是网格的行数和列数， $k$ 是建筑物的数量。每个建筑物都需要执行一次 BFS，每次 BFS 的时间复杂度为 $O(m \times n)$ 。
空间复杂度： $O(m \times n)$ ，需要额外的数组来存储距离信息和访问状态。