---

0302. 包含全部黑色像素的最小矩形

• 标签：深度优先搜索、广度优先搜索、数组、二分查找、矩阵
• 难度：困难

题目链接

• 0302. 包含全部黑色像素的最小矩形 - 力扣

题目大意

描述：

图片在计算机处理中往往是使用二维矩阵来表示的。

给定一个大小为 $m \times n$ 的二进制矩阵 $image$ 表示一张黑白图片，$0$ 代表白色像素，$1$ 代表黑色像素。

黑色像素相互连接，也就是说，图片中只会有一片连在一块儿的黑色像素。像素点是水平或竖直方向连接的。

给定两个整数 $x$ 和 $y$ 表示某一个黑色像素的位置。

要求：

请你找出包含全部黑色像素的最小矩形（与坐标轴对齐），并返回该矩形的面积。

你必须设计并实现一个时间复杂度低于 $O(m \times n)$ 的算法来解决此问题。

说明：

• $m == image.length$。
• $n == image[i].length$。
• $1 \le m, n \le 10^{3}$。
• $image[i][j]$ 为 '0' 或 '1'。
• $1 \le x \lt m$。
• $1 \le y \lt n$。
• $image[x][y] == '1'$。
• $image$ 中的黑色像素仅形成一个组件。

示例：

• 示例 1：

![](https://assets.leetcode.com/uploads/2021/03/14/pixel-grid.jpg)

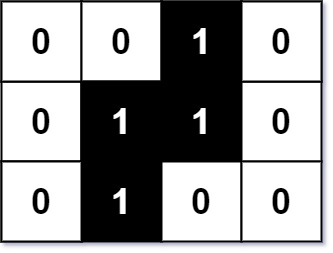
输入：image = [["0","0","1","0"],["0","1","1","0"],["0","1","0","0"]], x = 0, y = 2
输出：6

• 示例 2：

输入：image = [["1"]], x = 0, y = 0
输出：1

解题思路

思路 1：二分查找

核心思想：由于黑色像素是连通的，我们可以使用二分查找来找到包含所有黑色像素的最小矩形的边界。通过二分查找分别确定矩形的上、下、左、右边界。

算法步骤：

1. 确定边界范围：由于黑色像素是连通的，矩形的边界就是所有黑色像素的极值位置。

2. 二分查找上边界：在 $[0, x]$ 范围内二分查找最小的 $top$，使得第 $top$ 行包含黑色像素。

3. 二分查找下边界：在 $[x, m-1]$ 范围内二分查找最大的 $bottom$，使得第 $bottom$ 行包含黑色像素。

4. 二分查找左边界：在 $[0, y]$ 范围内二分查找最小的 $left$，使得第 $left$ 列包含黑色像素。

5. 二分查找右边界：在 $[y, n-1]$ 范围内二分查找最大的 $right$，使得第 $right$ 列包含黑色像素。

6. 计算面积：返回 $(bottom - top + 1) \times (right - left + 1)$。

思路 1：代码

class Solution:
    def minArea(self, image: List[List[str]], x: int, y: int) -> int:
        if not image or not image[0]:
            return 0
        
        m, n = len(image), len(image[0])
        
        # 二分查找上边界：找到最小的 top，使得第 top 行包含黑色像素
        def find_top():
            left, right = 0, x
            while left < right:
                mid = (left + right) // 2
                if any(image[mid][j] == '1' for j in range(n)):
                    right = mid
                else:
                    left = mid + 1
            return left
        
        # 二分查找下边界：找到最大的 bottom，使得第 bottom 行包含黑色像素
        def find_bottom():
            left, right = x, m - 1
            while left < right:
                mid = (left + right + 1) // 2  # 向上取整
                if any(image[mid][j] == '1' for j in range(n)):
                    left = mid
                else:
                    right = mid - 1
            return left
        
        # 二分查找左边界：找到最小的 left，使得第 left 列包含黑色像素
        def find_left():
            left, right = 0, y
            while left < right:
                mid = (left + right) // 2
                if any(image[i][mid] == '1' for i in range(m)):
                    right = mid
                else:
                    left = mid + 1
            return left
        
        # 二分查找右边界：找到最大的 right，使得第 right 列包含黑色像素
        def find_right():
            left, right = y, n - 1
            while left < right:
                mid = (left + right + 1) // 2  # 向上取整
                if any(image[i][mid] == '1' for i in range(m)):
                    left = mid
                else:
                    right = mid - 1
            return left
        
        # 找到矩形的四个边界
        top = find_top()
        bottom = find_bottom()
        left = find_left()
        right = find_right()
        
        # 计算并返回面积
        return (bottom - top + 1) * (right - left + 1)

思路 1：复杂度分析

• 时间复杂度：$O(m \log n + n \log m)$，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。每次二分查找的时间复杂度为 $O(\log k)$，其中 $k$ 是查找范围的大小。查找行边界需要 $O(m \log n)$ 时间，查找列边界需要 $O(n \log m)$ 时间。
• 空间复杂度：$O(1)$，只使用了常数额外空间，没有使用额外的数据结构。