---

0311. 稀疏矩阵的乘法

• 标签：数组、哈希表、矩阵
• 难度：中等

题目链接

• 0311. 稀疏矩阵的乘法 - 力扣

题目大意

描述：

给定两个「稀疏矩阵」：大小为 $m \times k$ 的稀疏矩阵 $mat1$ 和大小为 $k \times n$ 的稀疏矩阵 $mat2$。

要求：

返回 $mat1 \times mat2$ 的结果。你可以假设乘法总是可能的。

说明：

• $m == mat1.length$。
• $k == mat1[i].length == mat2.length$。
• $n == mat2[i].length$。
• $1 \le m, n, k \le 10^{3}$。
• $-10^{3} \le mat1[i][j], mat2[i][j] \le 10^{3}$。

示例：

• 示例 1：

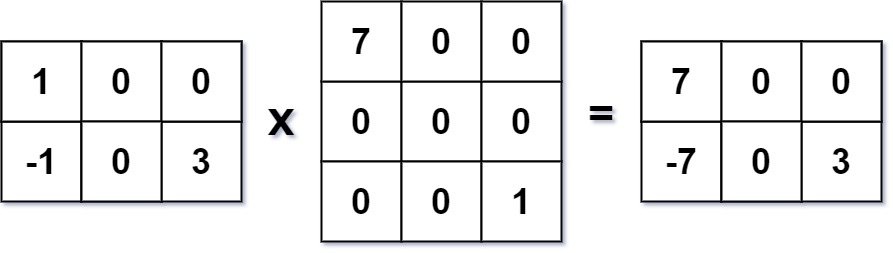
输入：mat1 = [[1,0,0],[-1,0,3]], mat2 = [[7,0,0],[0,0,0],[0,0,1]]
输出：[[7,0,0],[-7,0,3]]

• 示例 2：

输入：mat1 = [[0]], mat2 = [[0]]
输出：[[0]]

解题思路

思路 1：直接矩阵乘法

核心思想：按照矩阵乘法的定义，直接计算两个矩阵的乘积。对于结果矩阵 $result[i][j]$，它等于 $mat1$ 的第 $i$ 行与 $mat2$ 的第 $j$ 列对应元素乘积的和。

算法步骤：

1. 初始化结果矩阵：创建一个大小为 $m \times n$ 的结果矩阵 $result$，初始化为全零。

2. 三重循环计算：

   • 外层循环遍历 $mat1$ 的每一行 $i$（$0 \le i < m$）。
   • 中层循环遍历 $mat2$ 的每一列 $j$（$0 \le j < n$）。
   • 内层循环遍历公共维度 $k$（$0 \le k < k$）。

3. 计算乘积：对于每个位置 $(i, j)$，计算 $result[i][j] = \sum_{k=0}^{k-1} mat1[i][k] \times mat2[k][j]$。

4. 返回结果：返回计算完成的结果矩阵。

思路 1：代码

class Solution:
    def multiply(self, mat1: List[List[int]], mat2: List[List[int]]) -> List[List[int]]:
        # 获取矩阵维度
        m = len(mat1)        # mat1 的行数
        k = len(mat1[0])     # mat1 的列数，也是 mat2 的行数
        n = len(mat2[0])     # mat2 的列数
        
        # 初始化结果矩阵，大小为 m × n
        result = [[0] * n for _ in range(m)]
        
        # 三重循环计算矩阵乘法
        for i in range(m):           # 遍历 mat1 的每一行
            for j in range(n):       # 遍历 mat2 的每一列
                for l in range(k):   # 遍历公共维度
                    # 累加 mat1[i][l] * mat2[l][j] 到 result[i][j]
                    result[i][j] += mat1[i][l] * mat2[l][j]
        
        return result

思路 1：复杂度分析

• 时间复杂度：$O(m \times n \times k)$，其中 $m$ 是 $mat1$ 的行数，$n$ 是 $mat2$ 的列数，$k$ 是公共维度。需要三重循环遍历所有元素进行计算。
• 空间复杂度：$O(m \times n)$，用于存储结果矩阵，不包含输入矩阵的空间。