---

0457. 环形数组是否存在循环

• 标签：数组、哈希表、双指针
• 难度：中等

题目链接

• 0457. 环形数组是否存在循环 - 力扣

题目大意

描述：

存在一个不含 $0$ 的「环形」数组 $nums$，每个 $nums[i]$ 都表示位于下标 $i$ 的角色应该向前或向后移动的下标个数：

• 如果 $nums[i]$ 是正数，向前（下标递增方向）移动 $|nums[i]|$ 步。
• 如果 $nums[i]$ 是负数，向后（下标递减方向）移动 $|nums[i]|$ 步。

因为数组是「环形」的，所以可以假设从最后一个元素向前移动一步会到达第一个元素，而第一个元素向后移动一步会到达最后一个元素。

数组中的「循环」由长度为 $k$ 的下标序列 $seq$ 标识：

• 遵循上述移动规则将导致一组重复下标序列 $seq[0] \rightarrow seq[1] \rightarrow ... \rightarrow seq[k - 1] \rightarrow seq[0] \rightarrow ...$。
• 所有 $nums[seq[j]]$ 应当不是「全正」就是「全负」。
• $k > 1$。

要求：

如果 $nums$ 中存在循环，返回 $true$；否则，返回 $false$。

说明：

• $1 \le nums.length \le 5000$。

• $-10^{3} \le nums[i] \le 10^{3}$。

• $nums[i] \ne 0$。

• 进阶：你能设计一个时间复杂度为 $O(n)$ 且额外空间复杂度为 $O(1)$ 的算法吗？

示例：

• 示例 1：

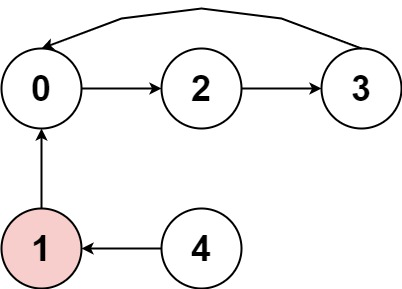
输入：nums = [2,-1,1,2,2]
输出：true
解释：图片展示了节点间如何连接。白色节点向前跳跃，而红色节点向后跳跃。
我们可以看到存在循环，按下标 0 -> 2 -> 3 -> 0 --> ...，并且其中的所有节点都是白色（以相同方向跳跃）。

• 示例 2：

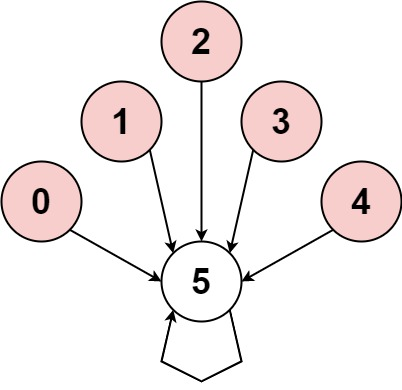
输入：nums = [-1,-2,-3,-4,-5,6]
输出：false
解释：图片展示了节点间如何连接。白色节点向前跳跃，而红色节点向后跳跃。
唯一的循环长度为 1，所以返回 false。

解题思路

思路 1：快慢指针检测

1. 使用快慢指针（Floyd 判圈算法）来检测循环。设置两个指针 $slow$ 和 $fast$，初始都指向同一个位置。
2. 慢指针每次移动 $1$ 步，快指针每次移动 $2$ 步。
3. 根据数组元素的值计算下一个位置：$next = (current + nums[current]) \bmod n$，如果结果为负数，需要加上 $n$ 来保证在有效范围内。
4. 在每次移动前需要检查：
   • 下一个位置的元素符号必须与起始方向相同（全正或全负）。
   • 不能出现自环（当前位置的下一个位置就是自己）。
5. 如果快慢指针相遇，说明存在有效循环，返回 $true$。
6. 对于每个起始位置都进行检测，如果找到一个有效循环就返回 $true$，否则继续检测下一个位置。

思路 1：代码

class Solution:
    def circularArrayLoop(self, nums: List[int]) -> bool:
        n = len(nums)
        
        def getNext(cur):
            """计算下一个位置"""
            return (cur + nums[cur]) % n
        
        # 遍历每个位置作为起始点
        for i in range(n):
            # 如果当前位置已经被访问过，跳过
            if nums[i] == 0:
                continue
            
            # 记录当前路径的方向（true 为正，false 为负）
            direction = nums[i] > 0
            
            # 使用快慢指针检测循环
            slow = i
            fast = i
            
            # 移动快慢指针直到相遇或违反条件
            while True:
                # 慢指针移动一步前，检查下一个位置的符号和自环
                slow_next = getNext(slow)
                if (nums[slow_next] > 0) != direction or slow == slow_next:
                    break
                slow = slow_next
                
                # 快指针移动两步，每步都需要检查
                fast_next = getNext(fast)
                if (nums[fast_next] > 0) != direction or fast == fast_next:
                    break
                fast = fast_next
                
                fast_next = getNext(fast)
                if (nums[fast_next] > 0) != direction or fast == fast_next:
                    break
                fast = fast_next
                
                # 如果快慢指针相遇，说明存在有效循环
                if slow == fast:
                    return True
            
            # 将当前路径上的所有元素标记为已访问
            # 这样可以避免重复检测
            temp = i
            while nums[temp] != 0 and (nums[temp] > 0) == direction:
                next_pos = getNext(temp)
                nums[temp] = 0  # 标记为已访问
                temp = next_pos
        
        return False

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是数组的长度。每个位置最多被访问一次，总的时间复杂度为 $O(n)$。
• 空间复杂度：$O(1)$，只使用了常数额外空间，没有使用额外的数据结构。