0407. 接雨水 II

ITCharge大约 3 分钟

---

0407. 接雨水 II

标签：广度优先搜索、数组、矩阵、堆（优先队列）
难度：困难

题目链接

0407. 接雨水 II - 力扣

题目大意

描述：

给定一个 $m \times n$ 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度。

要求：

请计算图中形状最多能接多少体积的雨水。

说明：

$m == heightMap.length$ 。
$n == heightMap[i].length$ 。
$1 \le m, n \le 200$ 。
$0 \le heightMap[i][j] \le 2 \times 10^{4}$ 。

示例：

示例 1：

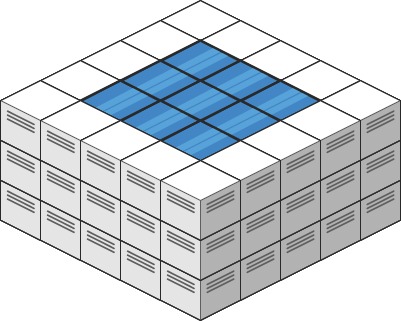
输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为 1+2+1=4。

示例 2：

输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10

解题思路

思路 1：优先队列（最小堆）+ BFS

核心思想：使用优先队列维护当前所有边界单元格的高度，从最矮的边界开始向内扩展，确保每个单元格都能接尽可能多的雨水。

算法步骤：

初始化优先队列 $min\_heap$ ，将所有边界单元格 $(i, j, heightMap[i][j])$ 加入队列，并用 $visited$ 数组标记。
初始化答案 $res = 0$ 。
当队列不为空时：
- 取出最小高度的单元格 $(i, j, height)$ 。
- 检查四个方向的邻居单元格 $(x, y)$ $(x, y)$ ：
  - 如果 $(x, y)$ 未被访问且合法，设其高度为 $h = heightMap[x][y]$ 。
  - 如果 $h < height$ ，则可以接雨水 $height - h$ ，累加到 $res$ 。
  - 更新 $heightMap[x][y] = \max(height, h)$ ，并将 $(x, y, heightMap[x][y])$ 加入队列。
  - 标记 $(x, y)$ 为已访问。
返回总接雨水量 $res$ 。

关键点：从最矮的边界开始处理，确保每个单元格的高度不低于其已处理邻居的最高边界，从而确定该单元格能接多少雨水。

思路 1：代码

import heapq
from typing import List

class Solution:
    def trapRainWater(self, heightMap: List[List[int]]) -> int:
        # 获取矩阵的行数和列数
        m, n = len(heightMap), len(heightMap[0])
        
        # 初始化结果
        res = 0
        
        # 初始化访问标记数组
        visited = [[False] * n for _ in range(m)]
        
        # 初始化优先队列（最小堆）
        min_heap = []
        
        # 将边界单元格加入队列
        for i in range(m):
            for j in range(n):
                # 如果是边界单元格
                if i == 0 or i == m - 1 or j == 0 or j == n - 1:
                    # 将 (高度, 行坐标, 列坐标) 加入队列
                    heapq.heappush(min_heap, (heightMap[i][j], i, j))
                    visited[i][j] = True
        
        # 定义四个方向
        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        
        # BFS 遍历
        while min_heap:
            # 取出最小高度的单元格
            height, i, j = heapq.heappop(min_heap)
            
            # 遍历四个方向
            for dx, dy in directions:
                x, y = i + dx, j + dy
                
                # 检查邻居是否合法且未访问
                if 0 <= x < m and 0 <= y < n and not visited[x][y]:
                    # 如果邻居高度小于当前边界高度，可以接雨水
                    if heightMap[x][y] < height:
                        res += height - heightMap[x][y]
                        # 更新邻居高度为当前边界高度
                        heightMap[x][y] = height
                    
                    # 将邻居加入队列
                    heapq.heappush(min_heap, (heightMap[x][y], x, y))
                    visited[x][y] = True
        
        return res

思路 1：复杂度分析

时间复杂度： $O(m \times n \times \log(m + n))$ 。其中 $m$ 和 $n$ 分别是矩阵的行数和列数。需要遍历所有单元格，每次堆操作的时间复杂度为 $O(\log(m + n))$ 。
空间复杂度： $O(m \times n)$ 。需要 $visited$ 数组和优先队列的空间，最坏情况下队列大小为 $O(m + n)$ 。