0545. 二叉树的边界

ITCharge大约 4 分钟

---

0545. 二叉树的边界

标签：树、深度优先搜索、二叉树
难度：中等

题目链接

0545. 二叉树的边界 - 力扣

题目大意

描述：

给定一棵二叉树的根节点 $root$ 。

要求：

按逆时针顺序返回边界节点的值。

说明：

二叉树的边界包含：
1. 根节点
2. 左边界：从根节点到最左侧叶子节点的路径（不包括叶子节点）
3. 所有叶子节点（从左到右）
4. 右边界：从最右侧叶子节点到根节点的路径（不包括根节点和叶子节点）
「左边界」是满足下述定义的节点集合：
- 根节点的左子节点在左边界中。如果根节点不含左子节点，那么左边界就为空。
- 如果一个节点在左边界中，并且该节点有左子节点，那么它的左子节点也在左边界中。
- 如果一个节点在左边界中，并且该节点不含左子节点，那么它的右子节点就在左边界中。
- 最左侧的叶节点「不在」左边界中。
「右边界」定义方式与左边界相同，只是将左替换成右。
「叶节点」是没有任何子节点的节点。对于此问题，根节点「不是」叶节点。
树中节点的数目在范围 $[1, 10^4]$ 内。
$-1000 \le Node.val \le 1000$ 。

示例：

示例 1：

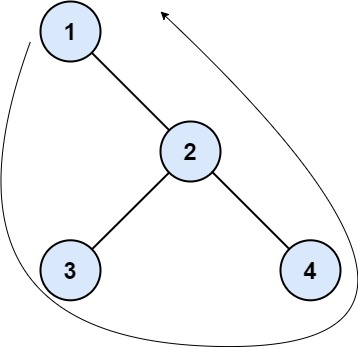
输入：root = [1,null,2,3,4]
输出：[1,3,4,2]
解释：
- 左边界为空，因为二叉树不含左子节点。
- 右边界是 [2] 。从根节点的右子节点开始的路径为 2 -> 4 ，但 4 是叶节点，所以右边界只有 2 。
- 叶节点从左到右是 [3,4] 。
按题目要求依序连接得到结果 [1] + [] + [3,4] + [2] = [1,3,4,2]。

示例 2：

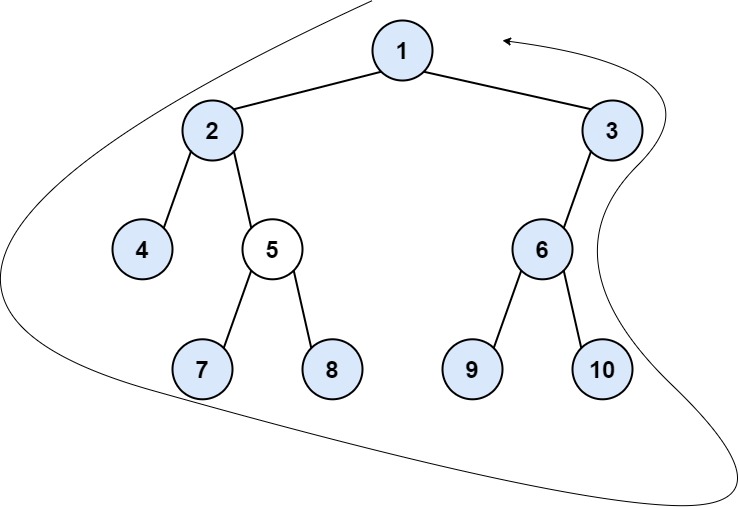
输入：root = [1,2,3,4,5,6,null,null,null,7,8,9,10]
输出：[1,2,4,7,8,9,10,6,3]
解释：
- 左边界为 [2] 。从根节点的左子节点开始的路径为 2 -> 4 ，但 4 是叶节点，所以左边界只有 2 。
- 右边界是 [3,6] ，逆序为 [6,3] 。从根节点的右子节点开始的路径为 3 -> 6 -> 10 ，但 10 是叶节点。
- 叶节点从左到右是 [4,7,8,9,10]
按题目要求依序连接得到结果 [1] + [2] + [4,7,8,9,10] + [6,3] = [1,2,4,7,8,9,10,6,3]。

解题思路

思路 1：分治 + DFS

将问题分解为三个部分：

找左边界：从根节点开始，优先走左子树，如果没有左子树则走右子树，直到叶子节点（不包括叶子）。
找所有叶子节点：使用 DFS 遍历，找到所有叶子节点。
找右边界：从根节点开始，优先走右子树，如果没有右子树则走左子树，直到叶子节点（不包括叶子），最后需要反转。

注意：根节点单独处理，避免重复。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def boundaryOfBinaryTree(self, root: Optional[TreeNode]) -> List[int]:
        if not root:
            return []
        
        # 判断是否为叶子节点
        def is_leaf(node):
            return node and not node.left and not node.right
        
        # 获取左边界（不包括叶子节点）
        def get_left_boundary(node):
            boundary = []
            while node:
                if not is_leaf(node):
                    boundary.append(node.val)
                # 优先走左子树，没有左子树则走右子树
                if node.left:
                    node = node.left
                else:
                    node = node.right
            return boundary
        
        # 获取所有叶子节点
        def get_leaves(node):
            if not node:
                return []
            if is_leaf(node):
                return [node.val]
            return get_leaves(node.left) + get_leaves(node.right)
        
        # 获取右边界（不包括叶子节点）
        def get_right_boundary(node):
            boundary = []
            while node:
                if not is_leaf(node):
                    boundary.append(node.val)
                # 优先走右子树，没有右子树则走左子树
                if node.right:
                    node = node.right
                else:
                    node = node.left
            return boundary[::-1]  # 反转
        
        # 如果根节点是叶子节点，直接返回
        if is_leaf(root):
            return [root.val]
        
        # 组合结果
        result = [root.val]
        result.extend(get_left_boundary(root.left))
        result.extend(get_leaves(root))
        result.extend(get_right_boundary(root.right))
        
        return result

思路 1：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 是树的节点数。每个节点最多被访问一次。
空间复杂度： $O(h)$ ，其中 $h$ 是树的高度，递归栈的深度。