---

0587. 安装栅栏

• 标签：几何、数组、数学
• 难度：困难

题目链接

• 0587. 安装栅栏 - 力扣

题目大意

描述：

给定一个数组 $trees$，其中 $trees[i] = [xi, yi]$ 表示树在花园中的位置。

要求：

用最短长度的绳子把整个花园围起来，因为绳子很贵。只有把所有的树都围起来，花园才围得很好。

返回恰好位于围栏周边的树木的坐标。

说明：

• $1 \le points.length \le 3000$。
• $points[i].length == 2$。
• $0 \le xi, yi \le 100$。
• 所有给定的点都是唯一的。

示例：

• 示例 1：

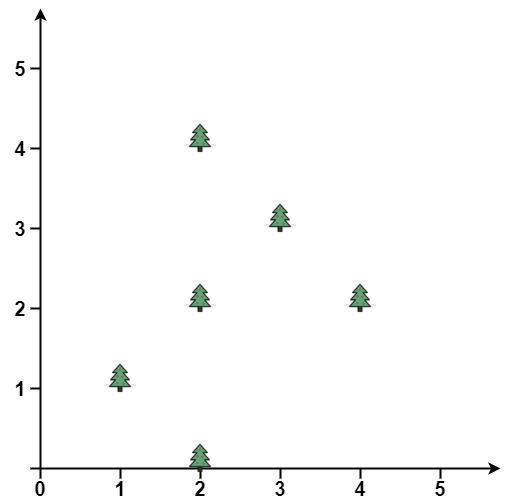
输入: points = [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出: [[1,1],[2,0],[3,3],[2,4],[4,2]]

• 示例 2：

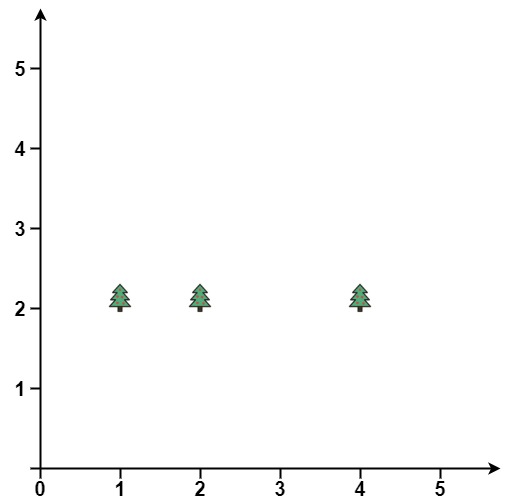
输入: points = [[1,2],[2,2],[4,2]]
输出: [[4,2],[2,2],[1,2]]

解题思路

思路 1：Graham 扫描算法（凸包）

这是一个经典的凸包问题。凸包是包含所有点的最小凸多边形。

Graham 扫描算法步骤：

1. 找到最左下角的点作为起点。
2. 按照极角排序其他点（相对于起点）。
3. 使用栈维护凸包的顶点。
4. 对于每个点，判断是否需要弹出栈顶（使用叉积判断转向）。
5. 如果是左转或共线，保留；如果是右转，弹出栈顶。

注意：题目要求返回所有在凸包边界上的点，包括共线的点。

思路 1：代码

class Solution:
    def outerTrees(self, trees: List[List[int]]) -> List[List[int]]:
        def cross(o, a, b):
            # 计算向量 OA 和 OB 的叉积
            return (a[0] - o[0]) * (b[1] - o[1]) - (a[1] - o[1]) * (b[0] - o[0])
        
        n = len(trees)
        if n < 4:
            return trees
        
        # 按照 x 坐标排序，x 相同则按 y 排序
        trees.sort()
        
        # 构建下凸包
        lower = []
        for p in trees:
            while len(lower) >= 2 and cross(lower[-2], lower[-1], p) < 0:
                lower.pop()
            lower.append(p)
        
        # 构建上凸包
        upper = []
        for p in reversed(trees):
            while len(upper) >= 2 and cross(upper[-2], upper[-1], p) < 0:
                upper.pop()
            upper.append(p)
        
        # 合并，去除重复点（首尾点会重复）
        return list(map(list, set(map(tuple, lower[:-1] + upper[:-1]))))

思路 1：复杂度分析

• 时间复杂度：$O(n \log n)$，主要是排序的时间复杂度，构建凸包是 $O(n)$。
• 空间复杂度：$O(n)$，需要存储凸包的顶点。