---

0510. 二叉搜索树中的中序后继 II

• 标签：树、二叉搜索树、二叉树
• 难度：中等

题目链接

• 0510. 二叉搜索树中的中序后继 II - 力扣

题目大意

描述：

给定一个二叉搜索树的节点 $node$，节点包含指向父节点的指针 $parent$。找到该节点在中序遍历中的后继节点。

节点的中序后继是中序遍历序列中该节点的下一个节点。如果不存在后继节点，返回 $null$。

要求：

返回给定节点的中序后继节点。

说明：

• 树中节点数在范围 $[1, 10^4]$ 内。
• $-10^5 \le Node.val \le 10^5$。
• 所有节点的值都是唯一的。

示例：

• 示例 1：

输入：tree = [2,1,3], node = 1
输出：2
解析：1 的中序后继结点是 2 。注意节点和返回值都是 Node 类型的。

• 示例 2：

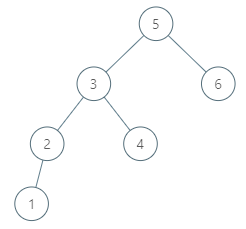
输入：tree = [5,3,6,2,4,null,null,1], node = 6
输出：null
解析：该结点没有中序后继，因此返回 null 。

解题思路

思路 1：分情况讨论

在二叉搜索树中，节点的中序后继有两种情况：

1. 如果节点有右子树：后继节点是右子树中最左边的节点。
2. 如果节点没有右子树：需要向上找父节点，直到找到一个节点是其父节点的左子节点，该父节点就是后继节点。

利用父节点指针，可以在不使用递归栈的情况下找到后继节点。

思路 1：代码

"""
# Definition for a Node.
class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None
"""

class Solution:
    def inorderSuccessor(self, node: 'Node') -> 'Optional[Node]':
        # 情况 1：如果有右子树，找右子树中最左边的节点
        if node.right:
            node = node.right
            while node.left:
                node = node.left
            return node
        
        # 情况 2：没有右子树，向上找父节点
        # 找到第一个是其父节点左子节点的节点
        while node.parent and node == node.parent.right:
            node = node.parent
        
        return node.parent

思路 1：复杂度分析

• 时间复杂度：$O(h)$，其中 $h$ 是树的高度。最坏情况下需要从叶子节点遍历到根节点。
• 空间复杂度：$O(1)$，只使用了常数额外空间。