0558. 四叉树交集

ITCharge大约 5 分钟

---

0558. 四叉树交集

标签：树、分治
难度：中等

题目链接

0558. 四叉树交集 - 力扣

题目大意

描述：

二进制矩阵中的所有元素不是 $0$ 就是 $1$ 。

给定两个四叉树， $quadTree1$ 和 $quadTree2$ 。其中 $quadTree1$ 表示一个 $n \times n$ 二进制矩阵，而 $quadTree2$ 表示另一个 $n \times n$ 二进制矩阵。

要求：

返回一个表示 $n \times n$ 二进制矩阵的四叉树，它是 $quadTree1$ 和 $quadTree2$ 所表示的两个二进制矩阵进行「按位逻辑或运算」的结果。

注意，当 $isLeaf$ 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制接受。

四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

$val$ ：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False；
$isLeaf$ : 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False。

class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

我们可以按以下步骤为二维区域构建四叉树：

如果当前网格的值相同（即，全为 $0$ 或者全为 $1$ ），将 $isLeaf$ 设为 True，将 $val$ 设为网格相应的值，并将四个子节点都设为 $Null$ 然后停止。
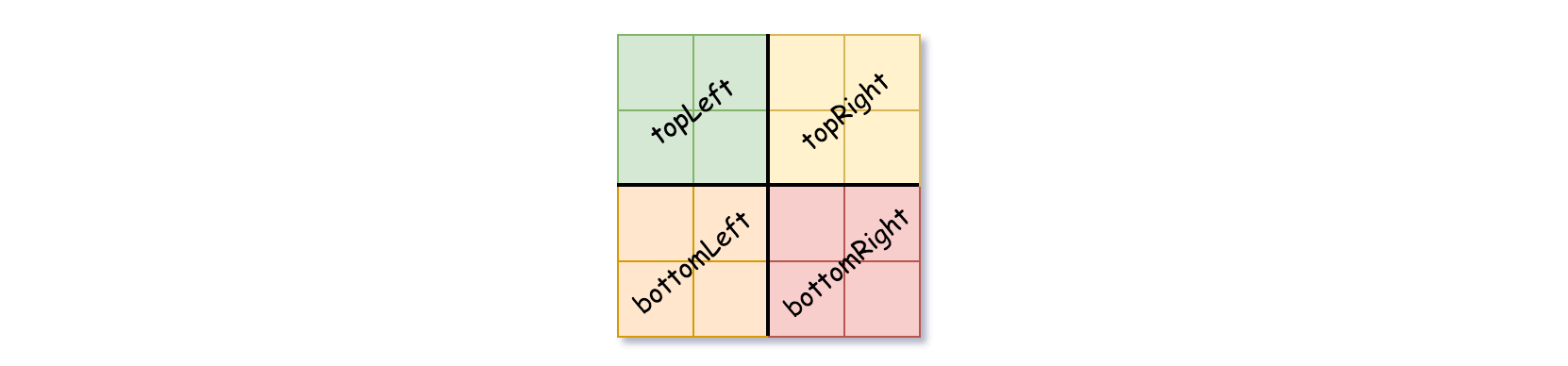
如果当前网格的值不同，将 $isLeaf$ 设为 False，将 $val$ 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
使用适当的子网格递归每个子节点。

说明：

四叉树格式：
- 输出为使用层序遍历后四叉树的序列化形式，其中 $null$ 表示路径终止符，其下面不存在节点。
- 它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 $[isLeaf, val]$ 。
- 如果 $isLeaf$ 或者 $val$ 的值为 True，则表示它在列表 $[isLeaf, val]$ 中的值为 1；如果 $isLeaf$ 或者 $val$ 的值为 False，则表示值为 0。
quadTree1 和 quadTree2 都是符合题目要求的四叉树，每个都代表一个 $n \times n$ 的矩阵。
$n == 2x$ ，其中 $0 \le x \le 9$ 。

示例：

示例 1：

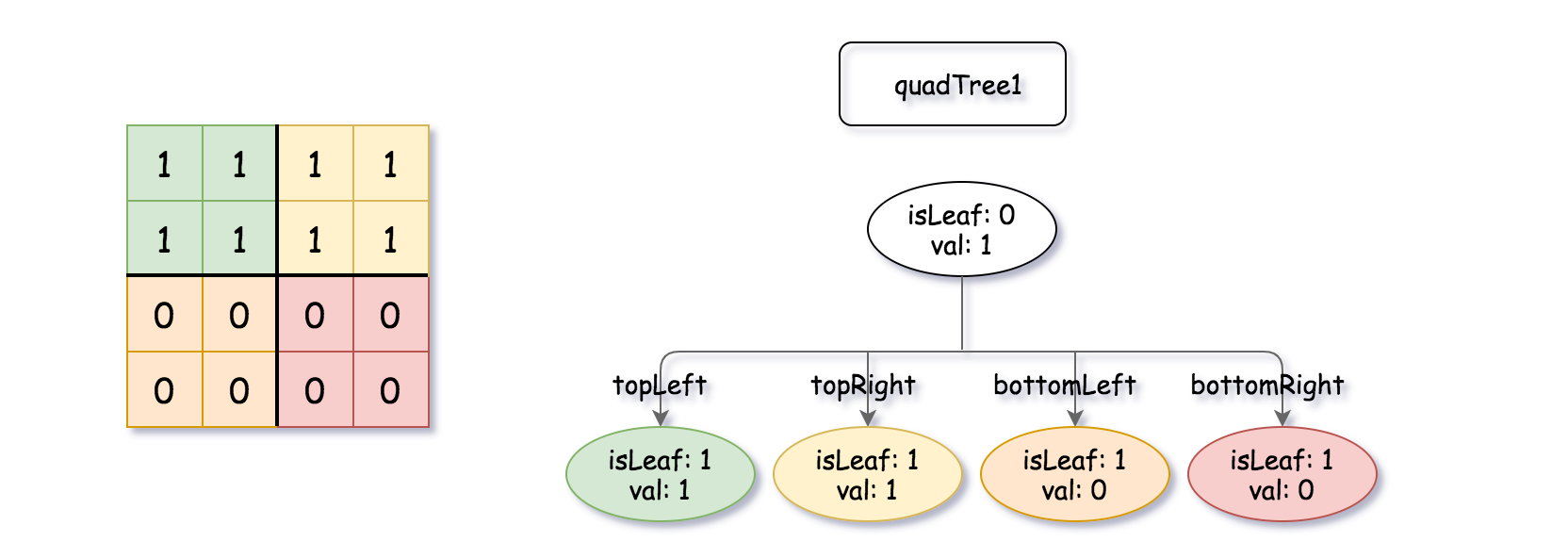
输入：quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
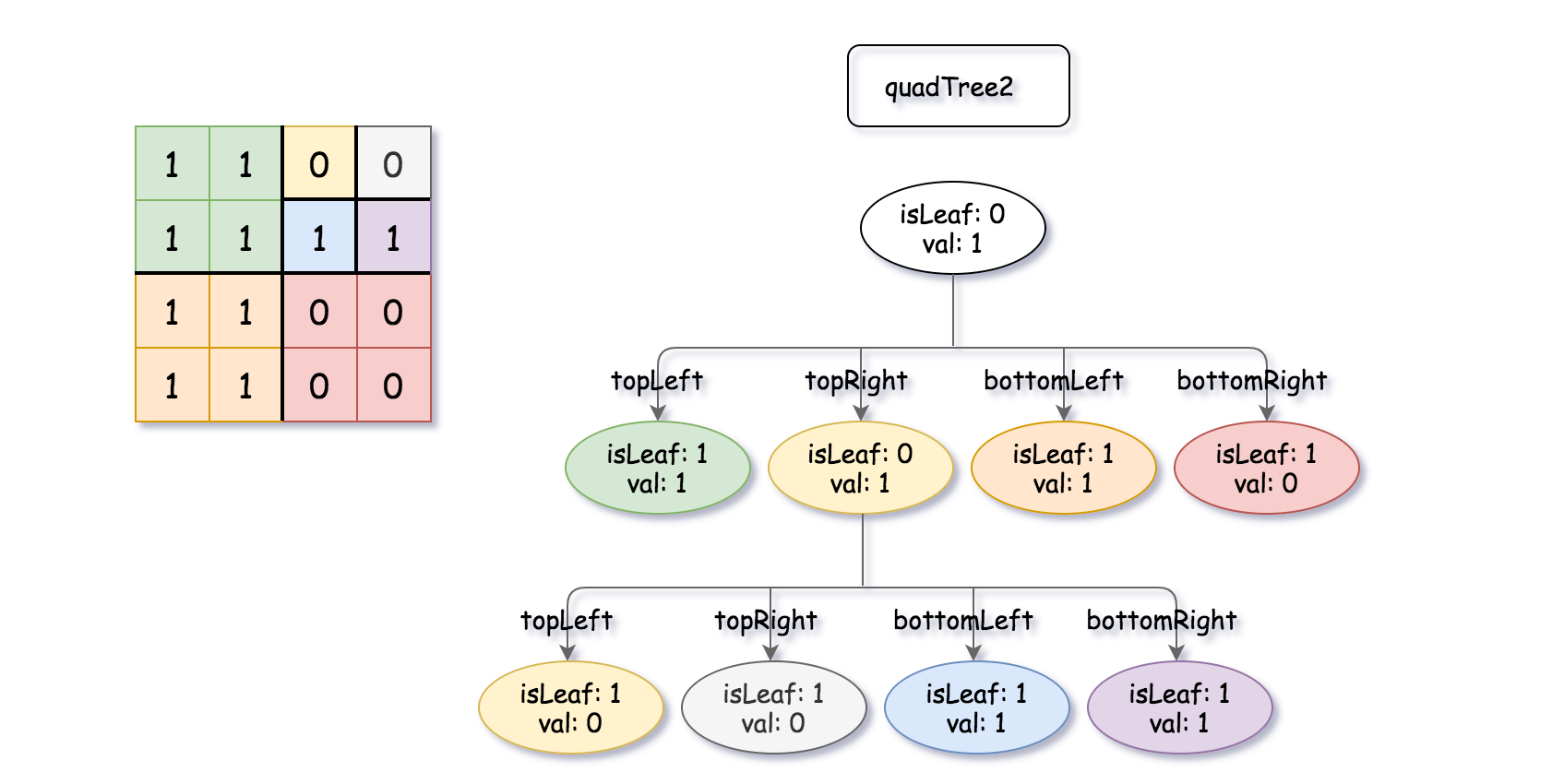
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
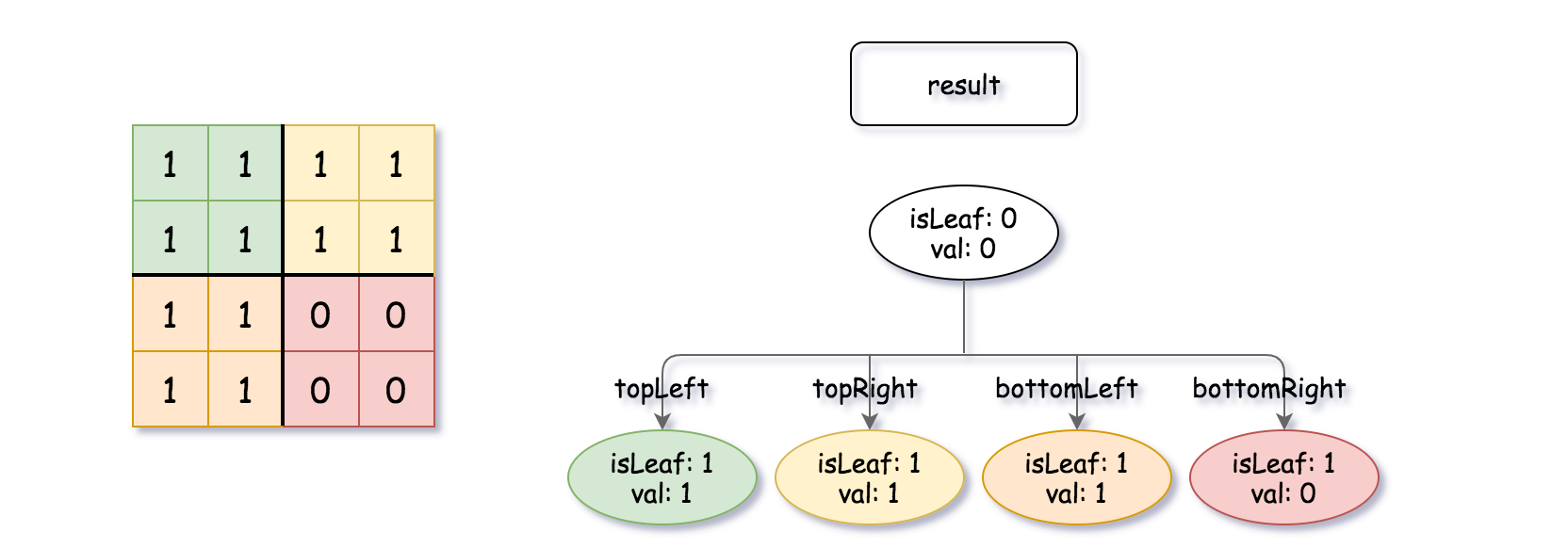
输出：[[0,0],[1,1],[1,1],[1,1],[1,0]]
解释：quadTree1 和 quadTree2 如上所示。由四叉树所表示的二进制矩阵也已经给出。
如果我们对这两个矩阵进行按位逻辑或运算，则可以得到下面的二进制矩阵，由一个作为结果的四叉树表示。
注意，我们展示的二进制矩阵仅仅是为了更好地说明题意，你无需构造二进制矩阵来获得结果四叉树。

示例 2：

输入：quadTree1 = [[1,0]]
, quadTree2 = [[1,0]]
输出：[[1,0]]
解释：两个数所表示的矩阵大小都为 1*1，值全为 0
结果矩阵大小为 1*1，值全为 0。

解题思路

思路 1：递归 + 分治

四叉树的逻辑或运算可以通过递归实现。对于两个四叉树节点，按照以下规则合并：

核心规则：

如果其中一个节点是叶子节点且值为 $True$ （表示全为 $1$ ），结果就是该节点。
如果其中一个节点是叶子节点且值为 $False$ （表示全为 $0$ ），结果就是另一个节点。
如果两个节点都是叶子节点：
- 如果值相同，返回任意一个。
- 如果值不同，返回值为 $True$ 的节点。
如果两个节点都不是叶子节点，递归处理四个子节点。
递归后检查四个子节点是否都是叶子节点且值相同，如果是则合并为一个叶子节点。

思路 1：代码

"""
# Definition for a QuadTree node.
class Node:
    def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):
        self.val = val
        self.isLeaf = isLeaf
        self.topLeft = topLeft
        self.topRight = topRight
        self.bottomLeft = bottomLeft
        self.bottomRight = bottomRight
"""

class Solution:
    def intersect(self, quadTree1: 'Node', quadTree2: 'Node') -> 'Node':
        # 如果 quadTree1 是叶子节点
        if quadTree1.isLeaf:
            # 如果值为 True，整个区域都是 1，返回 quadTree1
            if quadTree1.val:
                return quadTree1
            # 如果值为 False，结果取决于 quadTree2
            else:
                return quadTree2
        
        # 如果 quadTree2 是叶子节点
        if quadTree2.isLeaf:
            # 如果值为 True，整个区域都是 1，返回 quadTree2
            if quadTree2.val:
                return quadTree2
            # 如果值为 False，结果取决于 quadTree1
            else:
                return quadTree1
        
        # 两个都不是叶子节点，递归处理四个子节点
        top_left = self.intersect(quadTree1.topLeft, quadTree2.topLeft)
        top_right = self.intersect(quadTree1.topRight, quadTree2.topRight)
        bottom_left = self.intersect(quadTree1.bottomLeft, quadTree2.bottomLeft)
        bottom_right = self.intersect(quadTree1.bottomRight, quadTree2.bottomRight)
        
        # 检查四个子节点是否都是叶子节点且值相同
        if (top_left.isLeaf and top_right.isLeaf and 
            bottom_left.isLeaf and bottom_right.isLeaf and
            top_left.val == top_right.val == bottom_left.val == bottom_right.val):
            # 合并为一个叶子节点
            return Node(top_left.val, True, None, None, None, None)
        
        # 否则返回非叶子节点
        return Node(False, False, top_left, top_right, bottom_left, bottom_right)

思路 1：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 为两棵四叉树的节点总数，最坏情况下需要遍历所有节点。
空间复杂度： $O(\log n)$ ，递归调用栈的深度，最坏情况下为树的高度。