---

0533. 孤独像素 II

• 标签：数组、哈希表、矩阵
• 难度：中等

题目链接

• 0533. 孤独像素 II - 力扣

题目大意

描述：

给定一个由 'B' 和 'W' 组成的二维矩阵 $picture$ 和一个整数 $target$，其中 'B' 表示黑色像素，'W' 表示白色像素。

如果一个黑色像素 'B' 满足以下条件，则称其为孤独像素：

• 它所在的行恰好有 $target$ 个黑色像素。
• 它所在的列恰好有 $target$ 个黑色像素。
• 所有在同一行和同一列的黑色像素所在的行必须完全相同。

要求：

返回图片中孤独像素的数量。

说明：

• $m == picture.length$。
• $n == picture[i].length$。
• $1 \le m, n \le 200$。
• $picture[i][j]$ 为 'W' 或 'B'。
• $1 \le target \le \min(m, n)$。

示例：

• 示例 1：

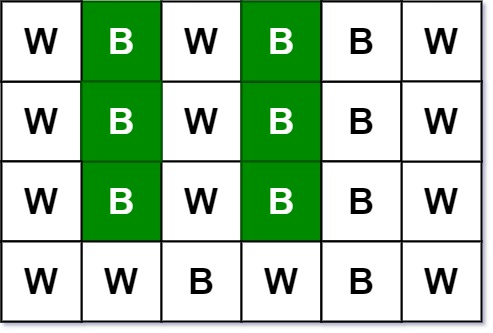
输入：picture = [["W","B","W","B","B","W"],["W","B","W","B","B","W"],["W","B","W","B","B","W"],["W","W","B","W","B","W"]], target = 3
输出：6
解释：所有绿色的 'B' 都是我们所求的像素(第 1 列和第 3 列的所有 'B' )
以行 r = 0 和列 c = 1 的 'B' 为例：
- 规则 1 ，行 r = 0 和列 c = 1 都恰好有 target = 3 个黑色像素 
- 规则 2 ，列 c = 1 的黑色像素分别位于行 0，行 1 和行 2。和行 r = 0 完全相同。

• 示例 2：

输入：picture = [["W","W","B"],["W","W","B"],["W","W","B"]], target = 1
输出：0

解题思路

思路 1：哈希表 + 行模式匹配

需要满足三个条件：

1. 行中恰好有 $target$ 个黑色像素。
2. 列中恰好有 $target$ 个黑色像素。
3. 同一列的所有黑色像素所在的行必须完全相同。

解题步骤：

1. 统计每行和每列的黑色像素数量。
2. 使用哈希表记录每种行模式出现的次数。
3. 对于每个黑色像素，检查是否满足所有条件。

思路 1：代码

class Solution:
    def findBlackPixel(self, picture: List[List[str]], target: int) -> int:
        if not picture or not picture[0]:
            return 0
        
        m, n = len(picture), len(picture[0])
        
        # 统计每行和每列的黑色像素数量
        row_count = [0] * m
        col_count = [0] * n
        
        for i in range(m):
            for j in range(n):
                if picture[i][j] == 'B':
                    row_count[i] += 1
                    col_count[j] += 1
        
        # 使用哈希表记录每种行模式及其出现次数
        from collections import defaultdict
        row_pattern = defaultdict(list)
        
        for i in range(m):
            if row_count[i] == target:
                pattern = ''.join(picture[i])
                row_pattern[pattern].append(i)
        
        # 统计孤独像素
        lonely_count = 0
        
        for pattern, rows in row_pattern.items():
            if len(rows) != target:
                continue
            
            # 检查每一列
            for j in range(n):
                if pattern[j] == 'B' and col_count[j] == target:
                    # 检查该列的所有黑色像素是否都在这些行中
                    valid = True
                    for i in range(m):
                        if picture[i][j] == 'B' and i not in rows:
                            valid = False
                            break
                    
                    if valid:
                        lonely_count += target
        
        return lonely_count

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。
• 空间复杂度：$O(m \times n)$，需要存储行模式和相关信息。