---

0562. 矩阵中最长的连续1线段

• 标签：数组、动态规划、矩阵
• 难度：中等

题目链接

• 0562. 矩阵中最长的连续1线段 - 力扣

题目大意

描述：

给定一个二维二进制矩阵 $mat$。

要求：

找出矩阵中最长的连续 $1$ 线段的长度。

这条线段可以是水平的、垂直的、对角线的或者反对角线的。

说明：

• $m == mat.length$。
• $n == mat[i].length$。
• $1 \le m, n \le 10^4$。
• $1 \le m \times n \le 10^4$。
• $mat[i][j]$ 不是 $0$ 就是 $1$。

示例：

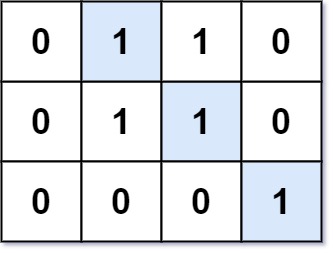
• 示例 1：

输入：mat = [[0,1,1,0],[0,1,1,0],[0,0,0,1]]
输出：3
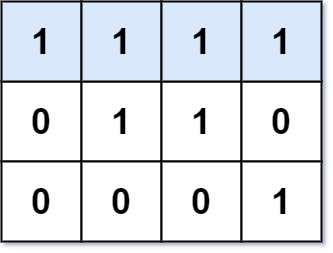
解释：最长的连续 1 线段是对角线方向的，长度为 3。

• 示例 2：

输入: mat = [[1,1,1,1],[0,1,1,0],[0,0,0,1]]
输出: 4
解释：最长的连续 1 线段是水平方向的，长度为 4。

解题思路

思路 1：动态规划

使用三维 DP 数组 $dp[i][j][d]$ 表示以位置 $(i, j)$ 结尾、方向为 $d$ 的最长连续 $1$ 的长度。

方向 $d$ 有 4 种：

• $0$：水平方向（从左到右）
• $1$：垂直方向（从上到下）
• $2$：对角线方向（从左上到右下）
• $3$：反对角线方向（从右上到左下）

状态转移：

• 如果 $mat[i][j] == 1$：
  • $dp[i][j][0] = dp[i][j-1][0] + 1$（水平）
  • $dp[i][j][1] = dp[i-1][j][1] + 1$（垂直）
  • $dp[i][j][2] = dp[i-1][j-1][2] + 1$（对角线）
  • $dp[i][j][3] = dp[i-1][j+1][3] + 1$（反对角线）
• 如果 $mat[i][j] == 0$：所有方向的 $dp$ 值都为 $0$

思路 1：代码

class Solution:
    def longestLine(self, mat: List[List[int]]) -> int:
        if not mat or not mat[0]:
            return 0
        
        m, n = len(mat), len(mat[0])
        # dp[i][j][d] 表示以 (i,j) 结尾、方向 d 的最长连续 1 长度
        # d: 0-水平, 1-垂直, 2-对角线, 3-反对角线
        dp = [[[0] * 4 for _ in range(n)] for _ in range(m)]
        max_len = 0
        
        for i in range(m):
            for j in range(n):
                if mat[i][j] == 1:
                    # 水平方向
                    dp[i][j][0] = dp[i][j-1][0] + 1 if j > 0 else 1
                    # 垂直方向
                    dp[i][j][1] = dp[i-1][j][1] + 1 if i > 0 else 1
                    # 对角线方向
                    dp[i][j][2] = dp[i-1][j-1][2] + 1 if i > 0 and j > 0 else 1
                    # 反对角线方向
                    dp[i][j][3] = dp[i-1][j+1][3] + 1 if i > 0 and j < n - 1 else 1
                    
                    # 更新最大值
                    max_len = max(max_len, max(dp[i][j]))
        
        return max_len

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。需要遍历整个矩阵。
• 空间复杂度：$O(m \times n)$，需要存储 DP 数组。可以优化到 $O(n)$ 使用滚动数组。