---

0529. 扫雷游戏

• 标签：深度优先搜索、广度优先搜索、数组、矩阵
• 难度：中等

题目链接

• 0529. 扫雷游戏 - 力扣

题目大意

描述：

让我们一起来玩扫雷游戏！

给定一个大小为 $m$ $x$ $n$ 二维字符矩阵 $board$ ，表示扫雷游戏的盘面，其中：

• 'M' 代表一个「未挖出的」地雷，
• 'E' 代表一个「未挖出的」空方块，
• 'B' 代表没有相邻（上，下，左，右，和所有4个对角线）地雷的「已挖出的」空白方块，
• 数字（'1' 到 '8'）表示有多少地雷与这块「已挖出的」方块相邻，
• 'X' 则表示一个「已挖出的」地雷。

给定一个整数数组 $click$，其中 $click = [clickr, clickc]$ 表示在所有「未挖出的」方块（'M' 或者 'E'）中的下一个点击位置（$clickr$ 是行下标，$clickc$ 是列下标）。

要求：

根据以下规则，返回相应位置被点击后对应的盘面：

1. 如果一个地雷（'M'）被挖出，游戏就结束了- 把它改为 'X'。
2. 如果一个 没有相邻地雷 的空方块（'E'）被挖出，修改它为（'B'），并且所有和其相邻的「未挖出的」方块都应该被递归地揭露。
3. 如果一个「至少与一个地雷相邻」的空方块（'E'）被挖出，修改它为数字（'1' 到 '8'），表示相邻地雷的数量。
4. 如果在此次点击中，若无更多方块可被揭露，则返回盘面。

说明：

• $m == board.length$。
• $n == board[i].length$。
• $1 \le m, n \le 50$。
• $board[i][j]$ 为 'M'、'E'、'B' 或数字 '1' 到 '8' 中的一个。
• $click.length == 2$。
• $0 \le clickr \lt m$。
• $0 \le clickc \lt n$。
• $board[clickr][clickc]$ 为 'M' 或 'E'。

示例：

• 示例 1：

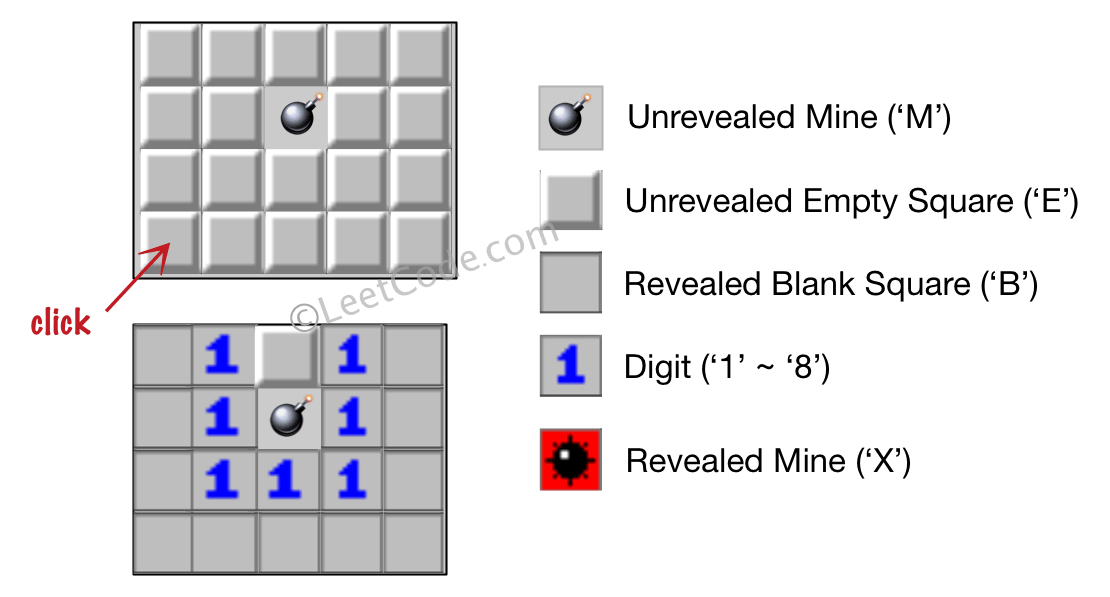
输入：board = [["E","E","E","E","E"],["E","E","M","E","E"],["E","E","E","E","E"],["E","E","E","E","E"]], click = [3,0]
输出：[["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]

• 示例 2：

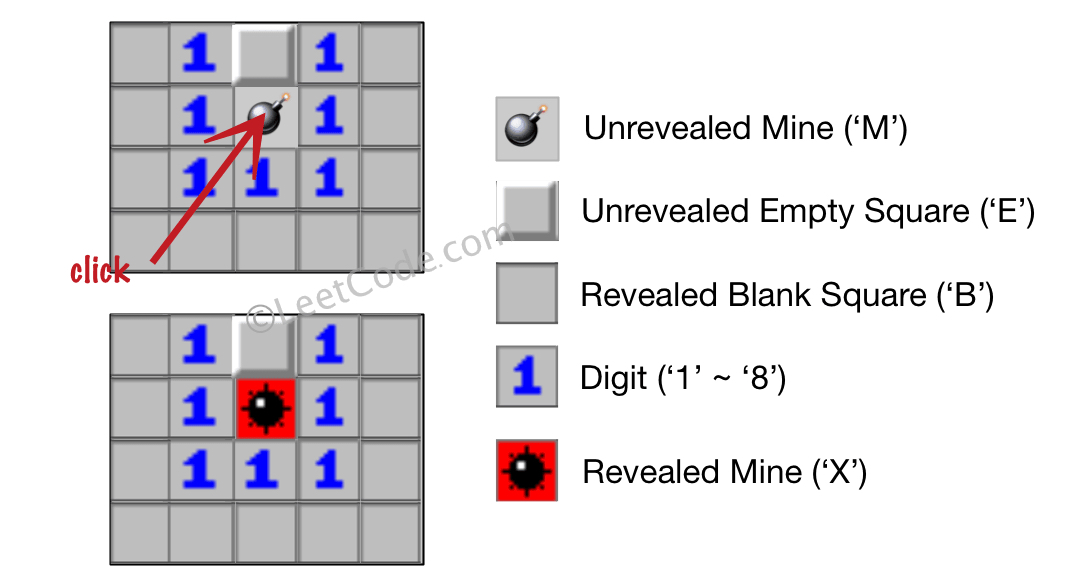
输入：board = [["B","1","E","1","B"],["B","1","M","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]], click = [1,2]
输出：[["B","1","E","1","B"],["B","1","X","1","B"],["B","1","1","1","B"],["B","B","B","B","B"]]

解题思路

思路 1：深度优先搜索（DFS）

这道题是经典的扫雷游戏模拟，需要根据点击位置进行不同的处理。

核心思路：

1. 如果点击位置是地雷 'M'，直接标记为 'X' 并返回。

2. 如果点击位置是空方块 'E'：

   • 统计周围 $8$ 个方向的地雷数量。
   • 如果周围有地雷，将当前位置标记为地雷数量（'1' 到 '8'）。
   • 如果周围没有地雷，标记为 'B'，并递归处理周围 $8$ 个方向的未挖出方块。

3. 使用 DFS 递归处理相邻的空方块。

思路 1：代码

class Solution:
    def updateBoard(self, board: List[List[str]], click: List[int]) -> List[List[str]]:
        m, n = len(board), len(board[0])
        x, y = click[0], click[1]
        
        # 8 个方向
        directions = [(-1, -1), (-1, 0), (-1, 1), (0, -1), 
                      (0, 1), (1, -1), (1, 0), (1, 1)]
        
        # 如果点击的是地雷，游戏结束
        if board[x][y] == 'M':
            board[x][y] = 'X'
            return board
        
        def dfs(i, j):
            # 统计周围地雷数量
            mine_count = 0
            for di, dj in directions:
                ni, nj = i + di, j + dj
                if 0 <= ni < m and 0 <= nj < n and board[ni][nj] == 'M':
                    mine_count += 1
            
            # 如果周围有地雷，标记数量
            if mine_count > 0:
                board[i][j] = str(mine_count)
            else:
                # 周围没有地雷，标记为 'B' 并递归处理相邻方块
                board[i][j] = 'B'
                for di, dj in directions:
                    ni, nj = i + di, j + dj
                    # 只处理未挖出的空方块
                    if 0 <= ni < m and 0 <= nj < n and board[ni][nj] == 'E':
                        dfs(ni, nj)
        
        # 从点击位置开始 DFS
        dfs(x, y)
        return board

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$，其中 $m$ 和 $n$ 分别为矩阵的行数和列数，最坏情况下需要遍历所有方块。
• 空间复杂度：$O(m \times n)$，递归调用栈的深度，最坏情况下为矩阵大小。