0598. 区间加法 II
大约 2 分钟
--- 
0598. 区间加法 II
- 标签:数组、数学
- 难度:简单
题目链接
题目大意
描述:
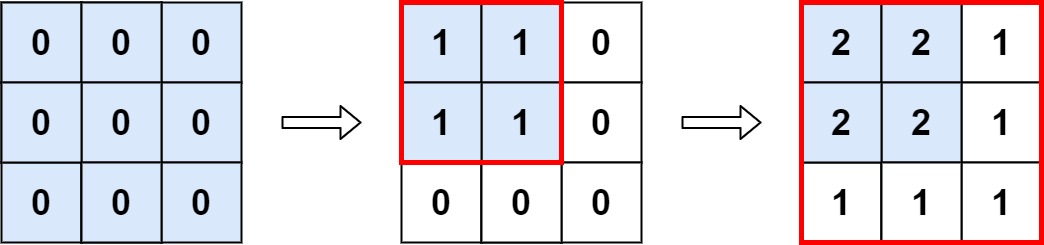
给定一个 的矩阵 和一个操作数组 。矩阵初始化时所有的单元格都为 。 意味着当所有的 和 时, 应该加 。
要求:
在执行完所有操作后,计算并返回「矩阵中最大整数的个数」。
说明:
- 。
- 。
- 。
- 。
- 。
示例:
- 示例 1:

输入: m = 3, n = 3,ops = [[2,2],[3,3]]
输出: 4
解释: M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。- 示例 2:
输入: m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
输出: 4解题思路
思路 1:找最小重叠区域
观察题目,每次操作 会将矩阵 中所有满足 且 的位置 加 1。这意味着每次操作都会影响从 到 的矩形区域。
执行所有操作后,被操作次数最多的位置就是所有操作都覆盖到的区域,即所有矩形区域的交集。这个交集区域的大小就是所有 的最小值和所有 的最小值组成的矩形。
因此,我们只需要找到所有操作中 的最小值 和 的最小值 ,那么最大整数的个数就是 。如果没有操作,则整个矩阵都是最大值,返回 。
思路 1:代码
class Solution:
def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:
# 如果没有操作,整个矩阵都是最大值
if not ops:
return m * n
# 找到所有操作中 a_i 和 b_i 的最小值
min_a = min(op[0] for op in ops)
min_b = min(op[1] for op in ops)
# 返回最小重叠区域的面积
return min_a * min_b思路 1:复杂度分析
- 时间复杂度:,其中 是 的长度,需要遍历所有操作找到最小值。
- 空间复杂度:,只使用了常数额外空间。