---

0566. 重塑矩阵

• 标签：数组、矩阵、模拟
• 难度：简单

题目链接

• 0566. 重塑矩阵 - 力扣

题目大意

描述：

在 MATLAB 中，有一个非常有用的函数 $reshape$ ，它可以将一个 $m \times n$ 矩阵重塑为另一个大小不同（$r \times c$）的新矩阵，但保留其原始数据。

给定一个由二维数组 $mat$ 表示的 $m \times n$ 矩阵，以及两个正整数 $r$ 和 $c$ ，分别表示想要的重构的矩阵的行数和列数。

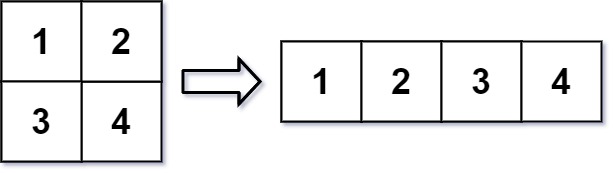
重构后的矩阵需要将原始矩阵的所有元素以相同的「行遍历顺序」填充。

要求：

如果具有给定参数的 $reshape$ 操作是可行且合理的，则输出新的重塑矩阵；否则，输出原始矩阵。

说明：

• $m == mat.length$。
• $n == mat[i].length$。
• $1 \le m, n \le 10^{3}$。
• $-10^{3} \le mat[i][j] \le 10^{3}$。
• $1 \le r, c \le 300$。

示例：

• 示例 1：

输入：mat = [[1,2],[3,4]], r = 1, c = 4
输出：[[1,2,3,4]]

• 示例 2：

输入：mat = [[1,2],[3,4]], r = 2, c = 4
输出：[[1,2],[3,4]]

解题思路

思路 1：一维展开再重塑

将 $m \times n$ 的矩阵重塑为 $r \times c$ 的矩阵，需要满足 $m \times n = r \times c$。如果不满足，返回原矩阵。

我们可以将原矩阵按行遍历顺序展开成一维数组，然后按照新的行列数重新组织。对于原矩阵中的元素 $mat[i][j]$，在一维数组中的索引为 $i \times n + j$。对于新矩阵中的位置 $(i', j')$，在一维数组中的索引为 $i' \times c + j'$。

因此，我们可以直接通过索引映射来填充新矩阵：$new\_mat[i'][j'] = mat[(i' \times c + j') // n][(i' \times c + j') \% n]$。

思路 1：代码

class Solution:
    def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        
        # 如果元素总数不匹配，返回原矩阵
        if m * n != r * c:
            return mat
        
        # 创建新矩阵
        new_mat = [[0] * c for _ in range(r)]
        
        # 按行遍历顺序填充新矩阵
        for i in range(r):
            for j in range(c):
                # 计算在一维数组中的索引
                idx = i * c + j
                # 映射回原矩阵的坐标
                new_mat[i][j] = mat[idx // n][idx % n]
        
        return new_mat

思路 1：复杂度分析

• 时间复杂度：$O(r \times c)$，需要遍历新矩阵的所有位置进行填充。
• 空间复杂度：$O(r \times c)$，需要创建新矩阵存储结果（不包括输入空间）。