0505. 迷宫 II

ITCharge大约 3 分钟

---

0505. 迷宫 II

标签：深度优先搜索、广度优先搜索、图、数组、矩阵、最短路、堆（优先队列）
难度：中等

题目链接

0505. 迷宫 II - 力扣

题目大意

描述：

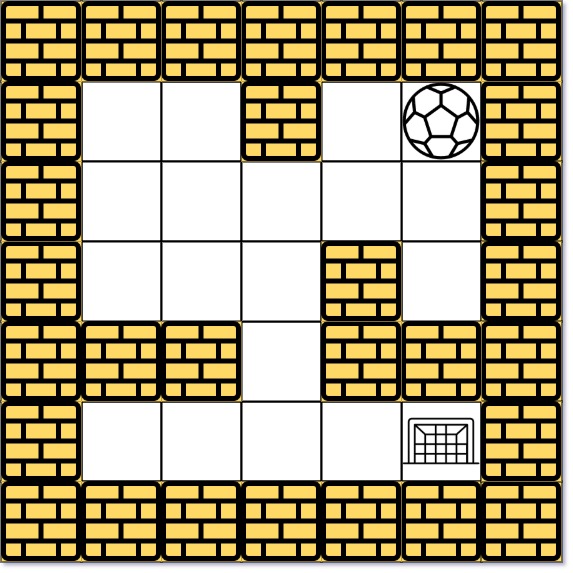
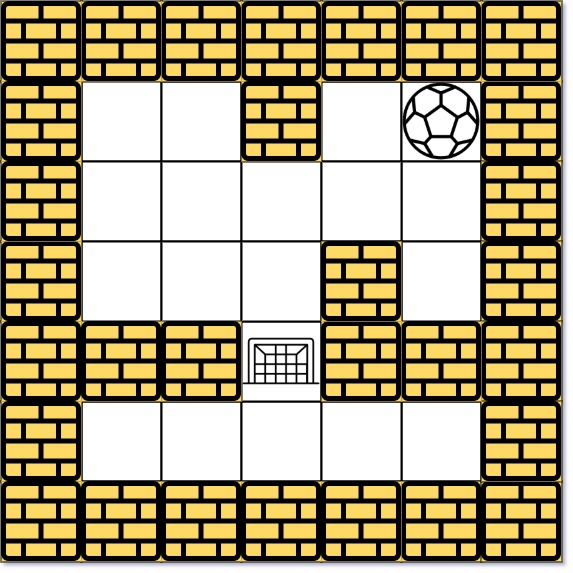
给定一个迷宫（二维数组） $maze$ ，其中 $0$ 表示空地， $1$ 表示墙壁。球可以向上、下、左、右四个方向滚动，但在碰到墙壁前不会停止滚动。当球停下时，可以选择下一个方向。

给定球的起始位置 $start$ 和目的地 $destination$ 。

要求：

返回球到达目的地的最短距离。如果球无法到达目的地，返回 $-1$ 。

说明：

距离是指球从起始位置（不包括）到终点（包括）经过的空地数量。
可以假设迷宫的边界都是墙。
$m == maze.length$ 。
$n == maze[i].length$ 。
$1 \le m, n \le 100$ 。
$maze[i][j]$ 是 $0$ 或 $1$ 。
$start.length == 2$ 。
$destination.length == 2$ 。
$0 \le start\_row, destination\_row < m$ 。
$0 \le start\_col, destination\_col < n$ 。
球和目的地都存在于一个空地中，它们最初不会处于相同的位置。

示例：

示例 1：

输入: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [4,4]
输出: 12
解析: 一条最短路径 : left -> down -> left -> down -> right -> down -> right。
总距离为 1 + 1 + 3 + 1 + 2 + 2 + 2 = 12。

示例 2：

输入: maze = [[0,0,1,0,0],[0,0,0,0,0],[0,0,0,1,0],[1,1,0,1,1],[0,0,0,0,0]], start = [0,4], destination = [3,2]
输出: -1
解析: 球不可能在目的地停下来。注意，你可以经过目的地，但不能在那里停下来。

解题思路

思路 1：Dijkstra 算法（优先队列 + BFS）

这是一个最短路径问题，可以使用 Dijkstra 算法求解。

关键点：

球会一直滚动直到碰到墙壁才停下
需要记录到达每个停止位置的最短距离
使用优先队列（最小堆）保证每次取出距离最小的位置

步骤：

使用优先队列存储 $(distance, row, col)$
使用 $dist$ 数组记录到达每个位置的最短距离
对于每个位置，尝试四个方向滚动，直到碰到墙壁
如果新的距离更短，更新并加入队列

思路 1：代码

import heapq

class Solution:
    def shortestDistance(self, maze: List[List[int]], start: List[int], destination: List[int]) -> int:
        m, n = len(maze), len(maze[0])
        
        # 距离数组，初始化为无穷大
        dist = [[float('inf')] * n for _ in range(m)]
        dist[start[0]][start[1]] = 0
        
        # 优先队列：(距离, 行, 列)
        pq = [(0, start[0], start[1])]
        
        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        
        while pq:
            d, x, y = heapq.heappop(pq)
            
            # 如果到达目的地
            if x == destination[0] and y == destination[1]:
                return d
            
            # 如果当前距离大于已记录的距离，跳过
            if d > dist[x][y]:
                continue
            
            # 尝试四个方向
            for dx, dy in directions:
                nx, ny = x, y
                steps = 0
                
                # 一直滚动直到碰到墙壁
                while 0 <= nx + dx < m and 0 <= ny + dy < n and maze[nx + dx][ny + dy] == 0:
                    nx += dx
                    ny += dy
                    steps += 1
                
                # 计算新的距离
                new_dist = d + steps
                
                # 如果找到更短的路径
                if new_dist < dist[nx][ny]:
                    dist[nx][ny] = new_dist
                    heapq.heappush(pq, (new_dist, nx, ny))
        
        # 无法到达目的地
        return -1

思路 1：复杂度分析

时间复杂度： $O(m \times n \times \log(m \times n))$ ，其中 $m$ 和 $n$ 是迷宫的行数和列数。每个位置最多入队一次，堆操作的时间复杂度为 $O(\log(m \times n))$ 。
空间复杂度： $O(m \times n)$ ，需要存储距离数组和优先队列。