0675. 为高尔夫比赛砍树

ITCharge大约 3 分钟

---

0675. 为高尔夫比赛砍树

标签：广度优先搜索、数组、矩阵、堆（优先队列）
难度：困难

题目链接

0675. 为高尔夫比赛砍树 - 力扣

题目大意

描述：

你被请来给一个要举办高尔夫比赛的树林砍树。树林由一个 $m \times n$ 的矩阵表示，在这个矩阵中：

$0$ 表示障碍，无法触碰
$1$ 表示地面，可以行走
比 $1$ 大的数表示有树的单元格，可以行走，数值表示树的高度

每一步，你都可以向上、下、左、右四个方向之一移动一个单位，如果你站的地方有一棵树，那么你可以决定是否要砍倒它。

你需要按照树的高度从低向高砍掉所有的树，每砍过一颗树，该单元格的值变为 $1$ （即变为地面）。

要求：

你将从 $(0, 0)$ 点开始工作，返回你砍完所有树需要走的最小步数。如果你无法砍完所有的树，返回 $-1$ 。

可以保证的是，没有两棵树的高度是相同的，并且你至少需要砍倒一棵树。

说明：

$m == forest.length$ 。
$n == forest[i].length$ 。
$1 \le m, n \le 50$ 。
$0 \le forest[i][j] \le 10^{9}$ 。

示例：

示例 1：

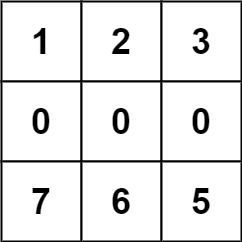
输入：forest = [[1,2,3],[0,0,4],[7,6,5]]
输出：6
解释：沿着上面的路径，你可以用 6 步，按从最矮到最高的顺序砍掉这些树。

示例 2：

输入：forest = [[1,2,3],[0,0,0],[7,6,5]]
输出：-1
解释：由于中间一行被障碍阻塞，无法访问最下面一行中的树。

解题思路

思路 1：BFS + 排序

思路 1：算法描述

这道题目要求按照树的高度从低到高砍树，返回砍完所有树需要走的最小步数。

我们可以将问题分解为两个子问题：

确定砍树的顺序：按照树的高度从低到高排序。
计算从一个位置到另一个位置的最短路径：使用 BFS。

具体步骤如下：

遍历矩阵，找到所有树的位置和高度，按照高度从低到高排序。
从起点 $(0, 0)$ 开始，依次前往每棵树的位置。
对于每次移动，使用 BFS 计算从当前位置到目标位置的最短路径。
如果无法到达某棵树，返回 $-1$ 。
累加所有移动的步数，返回总步数。

思路 1：代码

class Solution:
    def cutOffTree(self, forest: List[List[int]]) -> int:
        from collections import deque
        
        m, n = len(forest), len(forest[0])
        
        # 找到所有树的位置和高度
        trees = []
        for i in range(m):
            for j in range(n):
                if forest[i][j] > 1:
                    trees.append((forest[i][j], i, j))
        
        # 按照高度从低到高排序
        trees.sort()
        
        # BFS 计算从 (sr, sc) 到 (tr, tc) 的最短路径
        def bfs(sr, sc, tr, tc):
            if sr == tr and sc == tc:
                return 0
            
            queue = deque([(sr, sc, 0)])
            visited = {(sr, sc)}
            directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
            
            while queue:
                r, c, dist = queue.popleft()
                
                for dr, dc in directions:
                    nr, nc = r + dr, c + dc
                    
                    # 检查边界和障碍物
                    if 0 <= nr < m and 0 <= nc < n and (nr, nc) not in visited and forest[nr][nc] != 0:
                        if nr == tr and nc == tc:
                            return dist + 1
                        
                        queue.append((nr, nc, dist + 1))
                        visited.add((nr, nc))
            
            return -1  # 无法到达
        
        # 从起点开始，依次前往每棵树
        total_steps = 0
        sr, sc = 0, 0
        
        for _, tr, tc in trees:
            steps = bfs(sr, sc, tr, tc)
            if steps == -1:
                return -1
            total_steps += steps
            sr, sc = tr, tc
        
        return total_steps

思路 1：复杂度分析

时间复杂度： $O(m^2 \times n^2 \times t)$ ，其中 $m$ 和 $n$ 是矩阵的行数和列数， $t$ 是树的数量。每次 BFS 的时间复杂度为 $O(m \times n)$ ，需要进行 $t$ 次 BFS。
空间复杂度： $O(m \times n)$ 。BFS 需要使用队列和访问标记。