0663. 均匀树划分

ITCharge大约 2 分钟

---

0663. 均匀树划分

标签：树、深度优先搜索、二叉树
难度：中等

题目链接

0663. 均匀树划分 - 力扣

题目大意

描述：给你一棵二叉树的根节点 $root$ ，如果你可以通过去掉原始树上的一条边将树分成两棵节点值之和相等的子树，则返回 true。

要求：判断是否可以通过移除一条边将树分成两个节点值之和相等的子树。

说明：

树中节点数目在 $[1, 10^4]$ 范围内。
$-10^5 \le Node.val \le 10^5$ 。

示例：

示例 1：

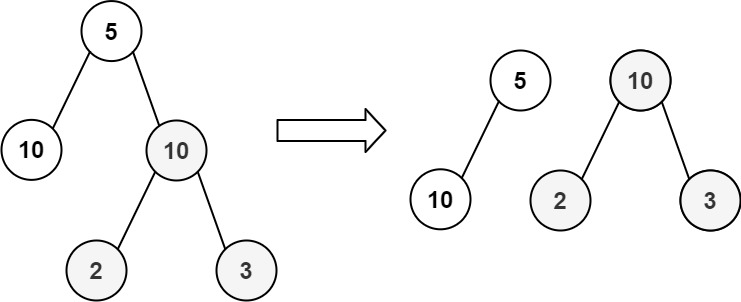
输入：root = [5,10,10,null,null,2,3]
输出：true

示例 2：

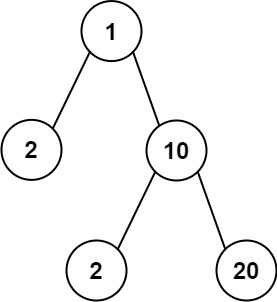
输入：root = [1,2,10,null,null,2,20]
输出：false
解释：在树上移除一条边无法将树分成两棵节点值之和相等的子树。

解题思路

思路 1：DFS + 后序遍历

思路 1：算法描述

判断是否可以通过移除一条边将树分成两个节点值之和相等的子树。

核心思路：

首先计算整棵树的总和 $total$ 。
如果 $total$ 是奇数，无法平分，返回 False。
使用 DFS 计算每个子树的和，如果某个子树的和等于 $total / 2$ ，说明可以分割。
注意：不能在根节点处分割（因为需要移除一条边）。

算法步骤：

计算整棵树的总和 $total$ 。
如果 $total$ 是奇数，返回 False。
使用 DFS 遍历树，计算每个子树的和：
- 如果某个非根子树的和等于 $total / 2$ ，返回 True。
如果遍历完没有找到，返回 False。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def checkEqualTree(self, root: Optional[TreeNode]) -> bool:
        # 计算整棵树的总和
        def get_sum(node):
            if not node:
                return 0
            return node.val + get_sum(node.left) + get_sum(node.right)
        
        total = get_sum(root)
        
        # 如果总和是奇数，无法平分
        if total % 2 != 0:
            return False
        
        target = total // 2
        self.found = False
        
        # DFS 检查每个子树的和
        def dfs(node, is_root):
            if not node:
                return 0
            
            left_sum = dfs(node.left, False)
            right_sum = dfs(node.right, False)
            current_sum = node.val + left_sum + right_sum
            
            # 如果不是根节点且子树和等于目标值
            if not is_root and current_sum == target:
                self.found = True
            
            return current_sum
        
        dfs(root, True)
        
        return self.found

思路 1：复杂度分析

时间复杂度： $O(n)$ ，其中 $n$ 是树的节点数，需要遍历树两次。
空间复杂度： $O(h)$ ，其中 $h$ 是树的高度，递归栈的深度。