---

0699. 掉落的方块

• 标签：线段树、数组、有序集合
• 难度：困难

题目链接

• 0699. 掉落的方块 - 力扣

题目大意

描述：

在二维平面上的 x 轴上，放置着一些方块。

给定一个二维整数数组 $positions$，其中 $positions[i] = [left\_i, sideLength\_i]$ 表示：第 $i$ 个方块边长为 $sideLength\_i$ ，其左侧边与 x 轴上坐标点 $left\_i$ 对齐。

每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落，直到着陆到「另一个正方形的顶边」或者是 x 轴上。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆，它就会固定在原地，无法移动。

在每个方块掉落后，你必须记录目前所有已经落稳的「方块堆叠的最高高度」。

要求：

返回一个整数数组 $ans$，其中 $ans[i]$ 表示在第 $i$ 块方块掉落后堆叠的最高高度。

说明：

• $1 \le positions.length \le 10^{3}$。
• $1 \le left_i \le 10^{8}$。
• $1 \le sideLength_i \le 10^{6}$。

示例：

• 示例 1：

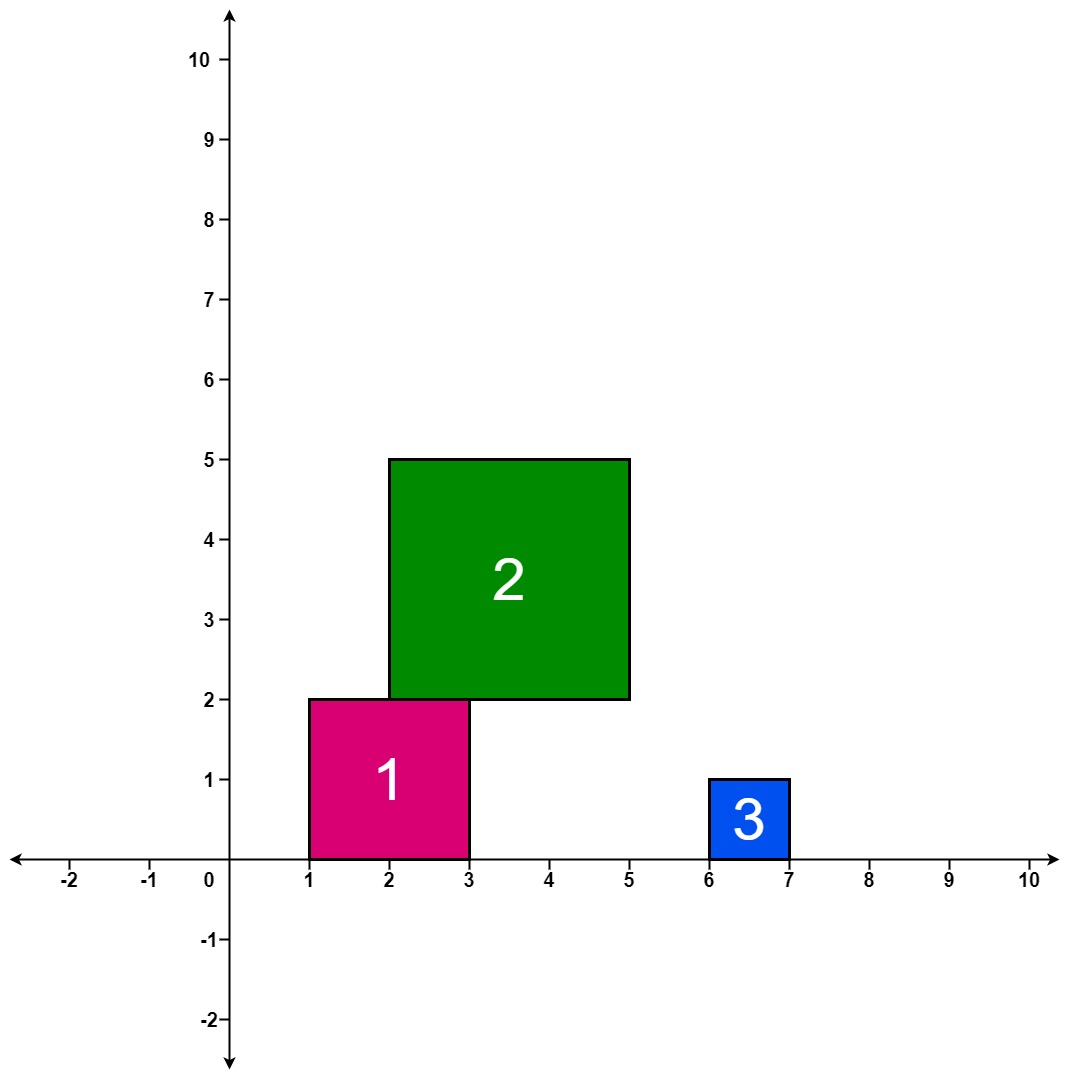
输入：positions = [[1,2],[2,3],[6,1]]
输出：[2,5,5]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 2 。
第 2 个方块掉落后，最高的堆叠由方块 1 和 2 组成，堆叠的最高高度为 5 。
第 3 个方块掉落后，最高的堆叠仍然由方块 1 和 2 组成，堆叠的最高高度为 5 。
因此，返回 [2, 5, 5] 作为答案。

• 示例 2：

输入：positions = [[100,100],[200,100]]
输出：[100,100]
解释：
第 1 个方块掉落后，最高的堆叠由方块 1 组成，堆叠的最高高度为 100 。
第 2 个方块掉落后，最高的堆叠可以由方块 1 组成也可以由方块 2 组成，堆叠的最高高度为 100 。
因此，返回 [100, 100] 作为答案。
注意，方块 2 擦过方块 1 的右侧边，但不会算作在方块 1 上着陆。

解题思路

思路 1：线段树 + 坐标压缩

这道题目要求模拟方块掉落的过程，记录每次掉落后的最大高度。由于坐标范围很大，需要使用坐标压缩。

1. 使用字典记录每个区间的当前高度。
2. 对于每个掉落的方块 $[left, sideLength]$：
   • 计算方块覆盖的区间 $[left, right]$，其中 $right = left + sideLength - 1$。
   • 查询该区间内的最大高度 $max\_height$。
   • 方块掉落后的高度为 $max\_height + sideLength$。
   • 更新该区间的高度。
   • 记录当前的最大高度。
3. 返回每次掉落后的最大高度列表。

思路 1：代码

class Solution:
    def fallingSquares(self, positions: List[List[int]]) -> List[int]:
        # 使用字典记录每个区间的高度
        heights = {}
        result = []
        max_height = 0
        
        for left, side_length in positions:
            right = left + side_length - 1
            
            # 查询 [left, right] 区间内的最大高度
            base_height = 0
            for (l, r), h in list(heights.items()):
                # 判断区间是否有重叠
                if not (r < left or l > right):
                    base_height = max(base_height, h)
            
            # 方块掉落后的高度
            new_height = base_height + side_length
            
            # 更新区间高度
            # 先删除被覆盖的区间
            keys_to_remove = []
            for (l, r) in list(heights.keys()):
                if left <= l and r <= right:
                    keys_to_remove.append((l, r))
            
            for key in keys_to_remove:
                del heights[key]
            
            # 添加新的区间
            heights[(left, right)] = new_height
            
            # 更新最大高度
            max_height = max(max_height, new_height)
            result.append(max_height)
        
        return result

思路 1：复杂度分析

• 时间复杂度：$O(n^2)$，其中 $n$ 是方块的数量。每次掉落需要遍历所有已有的区间。
• 空间复杂度：$O(n)$，需要使用字典存储区间高度信息。