---

0694. 不同岛屿的数量

• 标签：深度优先搜索、广度优先搜索、并查集、哈希表、哈希函数
• 难度：中等

题目链接

• 0694. 不同岛屿的数量 - 力扣

题目大意

描述：

给定一个非空 01 二维数组表示的网格，一个岛屿由四连通（上、下、左、右四个方向）的 $1$ 组成，你可以认为网格的四周被海水包围。

要求：

计算这个网格中共有多少个形状不同的岛屿。两个岛屿被认为是相同的，当且仅当一个岛屿可以通过平移变换（不可以旋转、翻转）和另一个岛屿重合。

说明：

• $m == grid.length$。
• $n == grid[i].length$。
• $1 \le m, n \le 50$。
• $grid[i][j]$ 仅包含 $0$ 或 $1$。

示例：

• 示例 1：

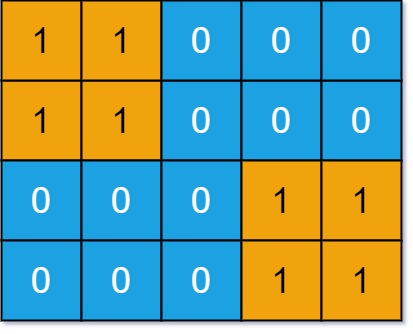
输入: grid = [[1,1,0,0,0],[1,1,0,0,0],[0,0,0,1,1],[0,0,0,1,1]]
输出：1

• 示例 2：

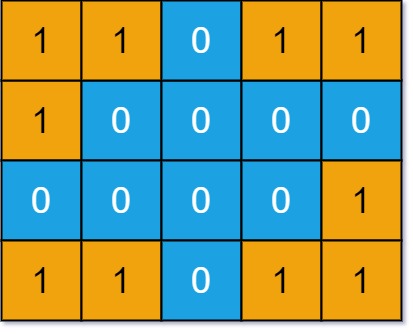
输入: grid = [[1,1,0,1,1],[1,0,0,0,0],[0,0,0,0,1],[1,1,0,1,1]]
输出: 3

解题思路

思路 1：深度优先搜索 + 哈希表

这道题目要求计算形状不同的岛屿数量。关键在于如何表示岛屿的形状。

核心思路：

• 使用深度优先搜索遍历每个岛屿。
• 记录岛屿的形状：以岛屿的第一个单元格为原点，记录其他单元格相对于原点的坐标。
• 将形状（坐标集合）转换为字符串或元组，存入哈希集合中。
• 最后返回哈希集合的大小。

算法步骤：

1. 遍历网格，找到每个岛屿的起点（值为 $1$ 的单元格）。
2. 对每个岛屿进行深度优先搜索，记录岛屿的形状（相对坐标）。
3. 将形状标准化（以第一个单元格为原点），转换为元组。
4. 将形状存入哈希集合。
5. 返回哈希集合的大小。

思路 1：代码

class Solution:
    def numDistinctIslands(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        visited = [[False] * n for _ in range(m)]
        shapes = set()
        
        def dfs(i, j, shape, base_i, base_j):
            """深度优先搜索，记录岛屿形状"""
            if i < 0 or i >= m or j < 0 or j >= n or visited[i][j] or grid[i][j] == 0:
                return
            
            visited[i][j] = True
            # 记录相对坐标
            shape.append((i - base_i, j - base_j))
            
            # 四个方向搜索
            dfs(i + 1, j, shape, base_i, base_j)
            dfs(i - 1, j, shape, base_i, base_j)
            dfs(i, j + 1, shape, base_i, base_j)
            dfs(i, j - 1, shape, base_i, base_j)
        
        # 遍历网格
        for i in range(m):
            for j in range(n):
                if grid[i][j] == 1 and not visited[i][j]:
                    shape = []
                    dfs(i, j, shape, i, j)
                    # 将形状转换为元组并存入集合
                    shapes.add(tuple(sorted(shape)))
        
        return len(shapes)

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$，其中 $m$ 和 $n$ 分别是网格的行数和列数。需要遍历整个网格。
• 空间复杂度：$O(m \times n)$。需要使用 $visited$ 数组和递归栈空间。