---

0666. 路径总和 IV

• 标签：树、深度优先搜索、数组、哈希表、二叉树
• 难度：中等

题目链接

• 0666. 路径总和 IV - 力扣

题目大意

描述：

对于一棵深度小于 $5$ 的树，可以用一组三位十进制整数来表示。给定一个由三位数组成的 递增 的数组 $nums$ 表示一棵深度小于 $5$ 的二叉树，对于每个整数：

• 百位上的数字表示这个节点的深度 $d$，$1 \le d \le 4$。
• 十位上的数字表示这个节点在当前层所在的位置 $p$，$1 \le p \le 8$。位置编号与一棵 满二叉树 的位置编号相同。
• 个位上的数字表示这个节点的权值 $v$，$0 \le v \le 9$。

要求：

返回从 根 到所有 叶子结点 的 路径之和。

保证 给定的数组表示一个有效的连接二叉树。

说明：

• $1 \le nums.length \le 15$。
• $110 \le nums[i] \le 489$。
• $nums$ 表示深度小于 $5$ 的有效二叉树。
• $nums$ 以升序排序。

示例：

• 示例 1：

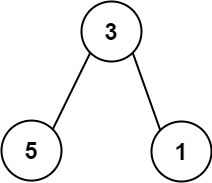
输入：nums = [113, 215, 221]
输出：12
解释：列表所表示的树如上所示。
路径和 = (3 + 5) + (3 + 1) = 12。

• 示例 2：

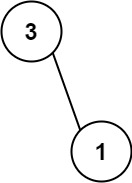
输入：nums = [113, 221]
输出：4
解释：列表所表示的树如上所示。
路径和 = (3 + 1) = 4。

解题思路

思路 1：DFS + 哈希表

思路 1：算法描述

给定一个特殊编码的二叉树，需要计算从根到所有叶子节点的路径和。

核心思路：

• 使用哈希表存储节点信息，键为 $(depth, position)$，值为节点的权值。
• 使用 DFS 遍历树，累加路径和。
• 判断叶子节点：左右子节点都不存在。

算法步骤：

1. 解析 nums 数组，构建哈希表存储节点信息。
2. 使用 DFS 从根节点开始遍历：
   • 累加当前路径和。
   • 如果是叶子节点，将路径和加入总和。
   • 否则递归遍历左右子节点。
3. 返回总和。

关键点：

• 对于深度为 $d$、位置为 $p$ 的节点，其左子节点位置为 $2p - 1$，右子节点位置为 $2p$，深度为 $d + 1$。

思路 1：代码

class Solution:
    def pathSum(self, nums: List[int]) -> int:
        # 构建哈希表，键为 (depth, position)，值为节点权值
        tree = {}
        for num in nums:
            depth = num // 100
            position = (num % 100) // 10
            value = num % 10
            tree[(depth, position)] = value
        
        self.total_sum = 0
        
        def dfs(depth, position, current_sum):
            # 当前节点的值
            if (depth, position) not in tree:
                return
            
            current_sum += tree[(depth, position)]
            
            # 计算左右子节点的位置
            left_pos = 2 * position - 1
            right_pos = 2 * position
            
            # 判断是否为叶子节点
            has_left = (depth + 1, left_pos) in tree
            has_right = (depth + 1, right_pos) in tree
            
            if not has_left and not has_right:
                # 叶子节点，累加路径和
                self.total_sum += current_sum
            else:
                # 递归遍历左右子树
                if has_left:
                    dfs(depth + 1, left_pos, current_sum)
                if has_right:
                    dfs(depth + 1, right_pos, current_sum)
        
        # 从根节点开始 DFS
        dfs(1, 1, 0)
        
        return self.total_sum

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是节点数量，每个节点访问一次。
• 空间复杂度：$O(n)$，哈希表和递归栈的空间开销。