---

0655. 输出二叉树

• 标签：树、深度优先搜索、广度优先搜索、二叉树
• 难度：中等

题目链接

• 0655. 输出二叉树 - 力扣

题目大意

描述：

给定一棵二叉树的根节点 $root$。

要求：

构造一个下标从 $0$ 开始、大小为 $m \times n$ 的字符串矩阵 $res$，用以表示树的「格式化布局」。

构造此格式化布局矩阵需要遵循以下规则：

• 树的「高度」为 $height$，矩阵的行数 $m$ 应该等于 $height + 1$。
• 矩阵的列数 $n$ 应该等于 $2^{height+1} - 1$。
• 「根节点」需要放置在「顶行」的「正中间」，对应位置为 $res[0][(n-1)/2]$。
• 对于放置在矩阵中的每个节点，设对应位置为 $res[r][c]$，将其左子节点放置在 $res[r+1][c-2^{height-r-1}]$，右子节点放置在 $res[r+1][c+2^{height-r-1}]$。
• 继续这一过程，直到树中的所有节点都妥善放置。
• 任意空单元格都应该包含空字符串 ""。

返回构造得到的矩阵 $res$。

说明：

• 树中节点数在范围 $[1, 2^{10}]$ 内。
• $-99 \le Node.val \le 99$。
• 树的深度在范围 $[1, 10]$ 内。

示例：

• 示例 1：

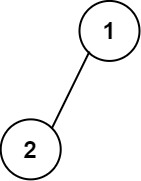
输入：root = [1,2]
输出：
[["","1",""],
 ["2","",""]]

• 示例 2：

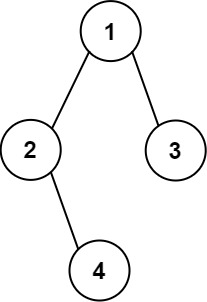
输入：root = [1,2,3,null,4]
输出：
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]

解题思路

思路 1：深度优先搜索

这道题目要求将二叉树按照特定格式输出到矩阵中。首先需要计算树的高度，然后根据高度确定矩阵的大小，最后使用 DFS 填充矩阵。

1. 计算树的高度 $height$。
2. 根据题目要求，矩阵的行数 $m = height + 1$，列数 $n = 2^{height + 1} - 1$。
3. 初始化矩阵，所有位置填充空字符串。
4. 使用 DFS 填充矩阵：
   • 根节点放在第 0 行的中间位置 $(n - 1) / 2$。
   • 对于位置 $(r, c)$ 的节点：
     • 左子节点放在 $(r + 1, c - 2^{height - r - 1})$。
     • 右子节点放在 $(r + 1, c + 2^{height - r - 1})$。
5. 返回矩阵。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
        # 计算树的高度
        def get_height(node):
            if not node:
                return -1
            return 1 + max(get_height(node.left), get_height(node.right))
        
        height = get_height(root)
        m = height + 1
        n = 2 ** (height + 1) - 1
        
        # 初始化矩阵
        result = [[""] * n for _ in range(m)]
        
        # DFS 填充矩阵
        def dfs(node, row, col):
            if not node:
                return
            
            result[row][col] = str(node.val)
            
            # 计算左右子节点的列偏移
            offset = 2 ** (height - row - 1)
            
            # 递归处理左右子树
            dfs(node.left, row + 1, col - offset)
            dfs(node.right, row + 1, col + offset)
        
        # 从根节点开始填充
        dfs(root, 0, (n - 1) // 2)
        
        return result

思路 1：复杂度分析

• 时间复杂度：$O(h \times 2^h)$，其中 $h$ 是树的高度。需要遍历所有节点，矩阵的大小为 $(h + 1) \times (2^{h + 1} - 1)$。
• 空间复杂度：$O(h \times 2^h)$，需要创建矩阵存储结果，递归调用栈的深度为 $O(h)$。