---

0685. 冗余连接 II

• 标签：深度优先搜索、广度优先搜索、并查集、图
• 难度：困难

题目链接

• 0685. 冗余连接 II - 力扣

题目大意

描述：

在本问题中，有根树指满足以下条件的「有向」图。该树只有一个根节点，所有其他节点都是该根节点的后继。

该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 $n$ 个节点（节点值不重复，从 $1$ 到 $n$）的树及一条附加的有向边构成。附加的边包含在 $1$ 到 $n$ 中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 $edges$。 每个元素是一对 $[ui, vi]$，用以表示「有向」图中连接顶点 $ui$ 和顶点 $vi$ 的边，其中 $ui$ 是 $vi$ 的一个父节点。

要求：

返回一条能删除的边，使得剩下的图是有 $n$ 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

说明：

• $n == edges.length$。
• $3 \le n \le 10^{3}$。
• $edges[i].length == 2$。
• $1 \le ui, vi \le n$。

示例：

• 示例 1：

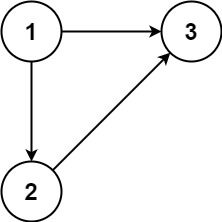
输入：edges = [[1,2],[1,3],[2,3]]
输出：[2,3]

• 示例 2：

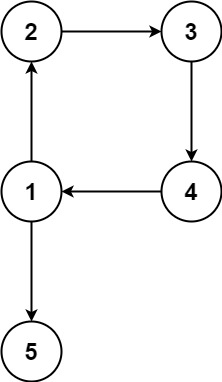
输入：edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
输出：[4,1]

解题思路

思路 1：并查集

这道题目是在有向图中找到一条可以删除的边，使得剩下的图是有根树。有向图中的有根树有以下特点：

1. 只有一个根节点（入度为 0）。
2. 除根节点外，其他节点的入度都为 1。

可能出现的情况：

1. 某个节点的入度为 2（有两个父节点）。
2. 图中存在环。

使用并查集来检测环，并记录入度为 2 的节点。

思路 1：代码

class Solution:
    def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        parent = list(range(n + 1))
        
        def find(x):
            if parent[x] != x:
                parent[x] = find(parent[x])
            return parent[x]
        
        def union(x, y):
            parent[find(x)] = find(y)
        
        # 记录每个节点的父节点
        in_degree = {}
        conflict_edge = None
        cycle_edge = None
        
        for u, v in edges:
            # 如果 v 已经有父节点，说明有冲突
            if v in in_degree:
                conflict_edge = [u, v]
            else:
                in_degree[v] = u
                
                # 检查是否形成环
                if find(u) == find(v):
                    cycle_edge = [u, v]
                else:
                    union(u, v)
        
        # 情况 1：没有冲突边，只有环
        if not conflict_edge:
            return cycle_edge
        
        # 情况 2：有冲突边
        # 如果没有环，删除冲突边
        if not cycle_edge:
            return conflict_edge
        
        # 情况 3：既有冲突边又有环
        # 删除导致冲突的第一条边
        return [in_degree[conflict_edge[1]], conflict_edge[1]]

思路 1：复杂度分析

• 时间复杂度：$O(n \times \alpha(n))$，其中 $n$ 是边的数量，$\alpha(n)$ 是阿克曼函数的反函数，可以认为是常数。
• 空间复杂度：$O(n)$，需要使用并查集和哈希表存储节点的父节点信息。