---

0787. K 站中转内最便宜的航班

• 标签：深度优先搜索、广度优先搜索、图、动态规划、最短路、堆（优先队列）
• 难度：中等

题目链接

• 0787. K 站中转内最便宜的航班 - 力扣

题目大意

描述：

有 $n$ 个城市通过一些航班连接。给你一个数组 $flights$，其中 $flights[i] = [from_i, to_i, price_i]$，表示该航班都从城市 $from_i$ 开始，以价格 $price_i$ 抵达 $to_i$。

现在给定所有的城市和航班，以及出发城市 $src$ 和目的地 $dst$。

要求：

找到出一条最多经过 $k$ 站中转的路线，使得从 $src$ 到 $dst$ 的「价格最便宜」，并返回该价格。如果不存在这样的路线，则输出 $-1$。

说明：

• $1 \le n \le 10^{3}$。
• $0 \le flights.length \le (n * (n - 1) / 2)$。
• $flights[i].length == 3$。
• $0 \le from_i, to_i \lt n$。
• $from_i \ne to_i$。
• $1 \le price_i \le 10^{4}$。
• 航班没有重复，且不存在自环。
• $0 \le src, dst, k \lt n$。
• $src \ne dst$。

示例：

• 示例 1：

输入: 
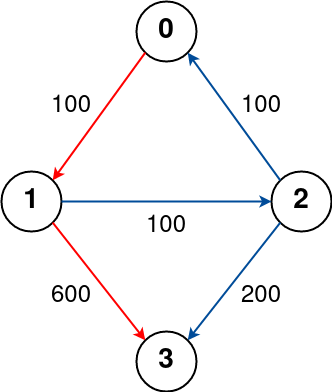
n = 4, flights = [[0,1,100],[1,2,100],[2,0,100],[1,3,600],[2,3,200]], src = 0, dst = 3, k = 1
输出: 700 
解释: 城市航班图如上
从城市 0 到城市 3 经过最多 1 站的最佳路径用红色标记，费用为 100 + 600 = 700。
请注意，通过城市 [0, 1, 2, 3] 的路径更便宜，但无效，因为它经过了 2 站。

• 示例 2：

输入: 
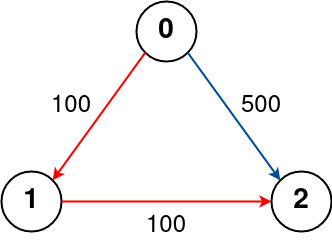
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1
输出: 200
解释: 
城市航班图如上
从城市 0 到城市 2 经过最多 1 站的最佳路径标记为红色，费用为 100 + 100 = 200。

解题思路

思路 1：动态规划（Bellman-Ford 算法）

这是一个带限制条件的最短路径问题。可以使用动态规划或 Bellman-Ford 算法求解。

状态定义：

• $dp[k][i]$ 表示经过最多 $k$ 次中转到达城市 $i$ 的最小花费。

状态转移：

• $dp[k][i] = \min(dp[k][i], dp[k-1][j] + price_{j \to i})$，其中 $j$ 是 $i$ 的前驱节点。

初始化：

• $dp[0][src] = 0$，其他为无穷大。

思路 1：代码

class Solution:
    def findCheapestPrice(self, n: int, flights: List[List[int]], src: int, dst: int, k: int) -> int:
        # 初始化 dp 数组
        INF = float('inf')
        dp = [INF] * n
        dp[src] = 0
        
        # 最多 k+1 次飞行（k 次中转）
        for _ in range(k + 1):
            # 使用临时数组避免状态覆盖
            new_dp = dp[:]
            
            for from_city, to_city, price in flights:
                if dp[from_city] != INF:
                    new_dp[to_city] = min(new_dp[to_city], dp[from_city] + price)
            
            dp = new_dp
        
        return dp[dst] if dp[dst] != INF else -1

思路 1：复杂度分析

• 时间复杂度：$O(k \times m)$，其中 $m$ 是航班数量。
• 空间复杂度：$O(n)$，$dp$ 数组的空间。