0749. 隔离病毒

ITCharge大约 4 分钟

---

0749. 隔离病毒

标签：深度优先搜索、广度优先搜索、数组、矩阵、模拟
难度：困难

题目链接

0749. 隔离病毒 - 力扣

题目大意

描述：

病毒扩散得很快，现在你的任务是尽可能地通过安装防火墙来隔离病毒。

假设世界由 $m \times n$ 的二维矩阵 $isInfected$ 组成， $isInfected[i][j] == 0$ 表示该区域未感染病毒，而 $isInfected[i][j] == 1$ 表示该区域已感染病毒。可以在任意 $2$ 个相邻单元之间的共享边界上安装一个防火墙（并且只有一个防火墙）。

每天晚上，病毒会从被感染区域向相邻未感染区域扩散，除非被防火墙隔离。现由于资源有限，每天你只能安装一系列防火墙来隔离其中一个被病毒感染的区域（一个区域或连续的一片区域），且该感染区域对未感染区域的威胁最大且保证唯一。

要求：

你需要努力使得最后有部分区域不被病毒感染，如果可以成功，那么返回需要使用的防火墙个数; 如果无法实现，则返回在世界被病毒全部感染时已安装的防火墙个数。

说明：

$m == isInfected.length$ 。
$n == isInfected[i].length$ 。
$1 \le m, n \le 50$ 。
$isInfected[i][j]$ 为 $0$ 或者 $1$ 。
在整个描述的过程中，总有一个相邻的病毒区域，它将在下一轮「严格地感染更多未受污染的方块」。

示例：

示例 1：

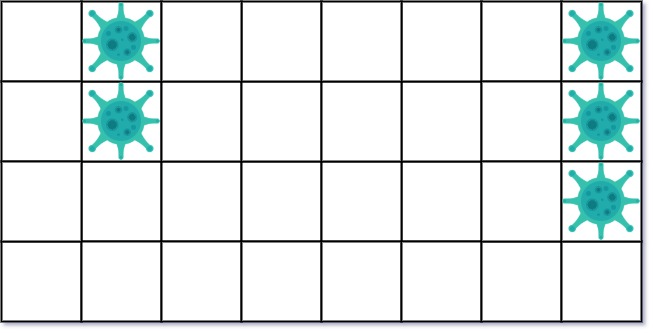
输入: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
输出: 10
解释:一共有两块被病毒感染的区域。
在第一天，添加 5 墙隔离病毒区域的左侧。病毒传播后的状态是:
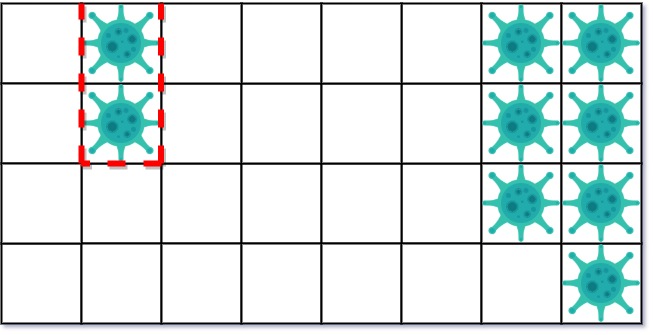
![](https://assets.leetcode.com/uploads/2021/06/01/virus12edited-grid.jpg)
第二天，在右侧添加 5 个墙来隔离病毒区域。此时病毒已经被完全控制住了。
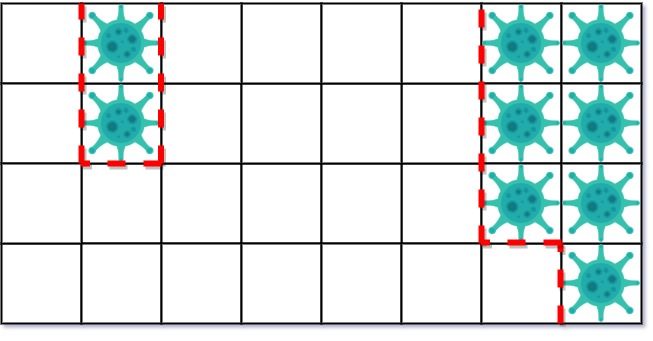![](https://assets.leetcode.com/uploads/2021/06/01/virus13edited-grid.jpg)

示例 2：

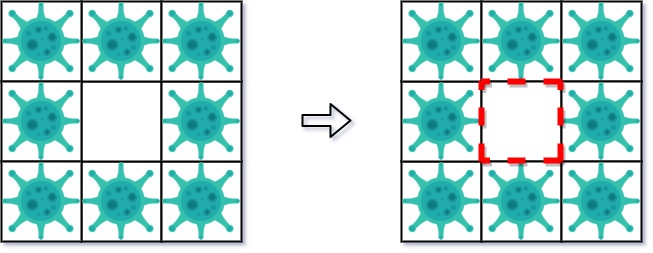
输入: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
输出: 4
解释: 虽然只保存了一个小区域，但却有四面墙。
注意，防火墙只建立在两个不同区域的共享边界上。

解题思路

思路 1：BFS + 模拟

这道题需要模拟病毒扩散和隔离的过程。

解题步骤：

每天找出所有被感染的区域（连通块）。
对于每个区域，计算其威胁值（能感染的未感染区域数量）和需要的防火墙数量。
选择威胁值最大的区域进行隔离，累加防火墙数量。
其他区域的病毒向相邻未感染区域扩散。
重复以上步骤，直到没有区域可以扩散。

实现细节：

使用 BFS 找出所有连通的感染区域。
对于每个区域，记录其能感染的未感染区域（去重）和需要的防火墙数量。
隔离后，将该区域标记为特殊值（如 $-1$ ），表示已隔离。

思路 1：代码

class Solution:
    def containVirus(self, isInfected: List[List[int]]) -> int:
        m, n = len(isInfected), len(isInfected[0])
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        total_walls = 0
        
        while True:
            visited = [[False] * n for _ in range(m)]
            regions = []  # 存储所有感染区域的信息
            
            # 找出所有感染区域
            for i in range(m):
                for j in range(n):
                    if isInfected[i][j] == 1 and not visited[i][j]:
                        # BFS 找出连通的感染区域
                        infected_cells = []  # 感染区域的所有单元格
                        threatened = set()  # 能感染的未感染区域
                        walls = 0  # 需要的防火墙数量
                        
                        queue = [(i, j)]
                        visited[i][j] = True
                        
                        while queue:
                            x, y = queue.pop(0)
                            infected_cells.append((x, y))
                            
                            for dx, dy in directions:
                                nx, ny = x + dx, y + dy
                                if 0 <= nx < m and 0 <= ny < n:
                                    if isInfected[nx][ny] == 1 and not visited[nx][ny]:
                                        queue.append((nx, ny))
                                        visited[nx][ny] = True
                                    elif isInfected[nx][ny] == 0:
                                        walls += 1
                                        threatened.add((nx, ny))
                        
                        regions.append((len(threatened), walls, infected_cells, threatened))
            
            # 如果没有感染区域，结束
            if not regions:
                break
            
            # 找出威胁值最大的区域
            regions.sort(reverse=True)
            threat_count, wall_count, infected_cells, threatened = regions[0]
            
            # 如果没有威胁，结束
            if threat_count == 0:
                break
            
            # 隔离威胁最大的区域
            total_walls += wall_count
            for x, y in infected_cells:
                isInfected[x][y] = -1  # 标记为已隔离
            
            # 其他区域扩散
            for i in range(1, len(regions)):
                for x, y in regions[i][3]:  # threatened
                    isInfected[x][y] = 1
        
        return total_walls

思路 1：复杂度分析

时间复杂度： $O((m \times n)^2)$ ，其中 $m$ 和 $n$ 是矩阵的行数和列数。最坏情况下需要进行 $O(m \times n)$ 轮模拟，每轮需要 $O(m \times n)$ 的时间。
空间复杂度： $O(m \times n)$ 。需要存储访问标记和区域信息。