---

0764. 最大加号标志

• 标签：数组、动态规划
• 难度：中等

题目链接

• 0764. 最大加号标志 - 力扣

题目大意

描述：

在一个 $n \times n$ 的矩阵 $grid$ 中，除了在数组 $mines$ 中给出的元素为 $0$，其他每个元素都为 $1$。$mines[i] = [xi, yi]$ 表示 $grid[xi][yi] == 0$。

要求：

返回 $grid$ 中包含 $1$ 的最大的「轴对齐」加号标志的阶数。如果未找到加号标志，则返回 $0$。

说明：

• 一个 $k$ 阶由 $1$ 组成的「轴对称加号标志」具有中心网格 $grid[r][c] == 1$，以及 $4$ 个从中心向上、向下、向左、向右延伸，长度为 $k - 1$，由 $1$ 组成的臂。注意，只有加号标志的所有网格要求为 $1$，别的网格可能为 $0$ 也可能为 $1$。
• $1 \le n \le 500$。
• $1 \le mines.length \le 5000$。
• $0 \le xi, yi \lt n$。
• 每一对 $(xi, yi)$ 都「不重复」。

示例：

• 示例 1：

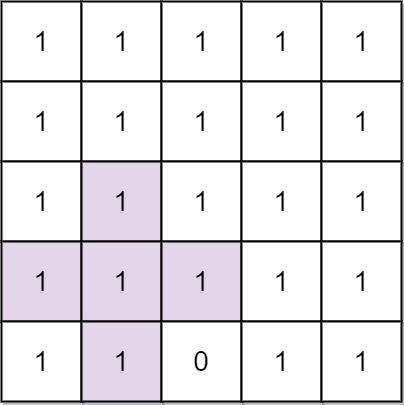
输入: n = 5, mines = [[4, 2]]
输出: 2
解释: 在上面的网格中，最大加号标志的阶只能是2。一个标志已在图中标出。

• 示例 2：

输入: n = 1, mines = [[0, 0]]
输出: 0
解释: 没有加号标志，返回 0 。

解题思路

思路 1：动态规划

这道题要求计算每个位置能形成的最大加号标志的阶数。

解题步骤：

1. 首先将所有位置初始化为 $1$，将 $mines$ 中的位置标记为 $0$。
2. 对于每个位置 $(i, j)$，计算其四个方向（上、下、左、右）连续 $1$ 的个数。
3. 定义 $dp[i][j]$ 表示位置 $(i, j)$ 能形成的最大加号标志的阶数。
4. $dp[i][j] = \min(\text{上}, \text{下}, \text{左}, \text{右})$，即四个方向中最小的连续 $1$ 的个数。
5. 返回所有 $dp[i][j]$ 中的最大值。

优化：可以在一次遍历中同时计算四个方向的连续 $1$ 的个数。

思路 1：代码

class Solution:
    def orderOfLargestPlusSign(self, n: int, mines: List[List[int]]) -> int:
        # 初始化所有位置为 n（表示最多可以延伸 n 个单位）
        dp = [[n] * n for _ in range(n)]
        
        # 将 mines 中的位置标记为 0
        banned = set(map(tuple, mines))
        for x, y in banned:
            dp[x][y] = 0
        
        # 计算每个位置四个方向的最小连续 1 的个数
        for i in range(n):
            # 从左到右
            left = 0
            # 从右到左
            right = 0
            # 从上到下
            up = 0
            # 从下到上
            down = 0
            
            for j in range(n):
                # 从左到右
                left = 0 if (i, j) in banned else left + 1
                dp[i][j] = min(dp[i][j], left)
                
                # 从右到左
                right = 0 if (i, n - 1 - j) in banned else right + 1
                dp[i][n - 1 - j] = min(dp[i][n - 1 - j], right)
                
                # 从上到下
                up = 0 if (j, i) in banned else up + 1
                dp[j][i] = min(dp[j][i], up)
                
                # 从下到上
                down = 0 if (n - 1 - j, i) in banned else down + 1
                dp[n - 1 - j][i] = min(dp[n - 1 - j][i], down)
        
        # 返回最大值
        return max(max(row) for row in dp)

思路 1：复杂度分析

• 时间复杂度：$O(n^2)$，其中 $n$ 是矩阵的边长。需要遍历矩阵四次。
• 空间复杂度：$O(n^2)$。需要存储 $dp$ 数组和 $banned$ 集合。