---

0773. 滑动谜题

• 标签：广度优先搜索、记忆化搜索、数组、动态规划、回溯、矩阵
• 难度：困难

题目链接

• 0773. 滑动谜题 - 力扣

题目大意

描述：

在一个 $2 \times 3$ 的板上（board）有 $5$ 块砖瓦，用数字 $1 \sim 5$ 来表示, 以及一块空缺用 $0$ 来表示。一次「移动」定义为选择 $0$ 与一个相邻的数字（上下左右）进行交换.

最终当板 $board$ 的结果是 $[[1,2,3],[4,5,0]]$ 谜板被解开。

给定一个谜板的初始状态 $board$。

要求：

返回最少可以通过多少次移动解开谜板，如果不能解开谜板，则返回 $-1$。

说明：

• $board.length == 2$。
• $board[i].length == 3$。
• $0 \le board[i][j] \le 5$。
• $board[i][j]$ 中每个值都不同。

示例：

• 示例 1：

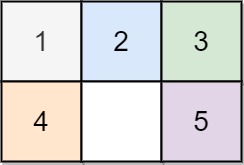
输入：board = [[1,2,3],[4,0,5]]
输出：1
解释：交换 0 和 5 ，1 步完成

• 示例 2：

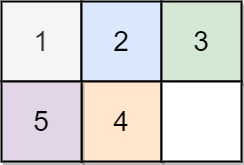
输入：board = [[1,2,3],[5,4,0]]
输出：-1
解释：没有办法完成谜板

解题思路

思路 1：BFS（广度优先搜索）

将滑动谜题看作状态搜索问题，使用 BFS 找到从初始状态到目标状态的最短路径。

实现步骤：

1. 将二维数组转换为字符串表示状态。
2. 目标状态为 "123450"。
3. 使用 BFS，每次找到 0 的位置，尝试与相邻位置交换：
   • 预先定义每个位置可以移动到的相邻位置。
   • 位置 $0, 1, 2, 3, 4, 5$ 分别对应二维数组的 $(0,0), (0,1), (0,2), (1,0), (1,1), (1,2)$。
4. 使用集合记录访问过的状态，避免重复。
5. 返回到达目标状态的最小步数。

思路 1：代码

class Solution:
    def slidingPuzzle(self, board: List[List[int]]) -> int:
        from collections import deque
        
        # 将二维数组转换为字符串
        start = ''.join(str(board[i][j]) for i in range(2) for j in range(3))
        target = "123450"
        
        if start == target:
            return 0
        
        # 每个位置可以移动到的相邻位置
        neighbors = {
            0: [1, 3],
            1: [0, 2, 4],
            2: [1, 5],
            3: [0, 4],
            4: [1, 3, 5],
            5: [2, 4]
        }
        
        # BFS
        queue = deque([(start, 0)])  # (状态, 步数)
        visited = {start}
        
        while queue:
            state, steps = queue.popleft()
            
            # 找到 0 的位置
            zero_pos = state.index('0')
            
            # 尝试移动到相邻位置
            for next_pos in neighbors[zero_pos]:
                # 交换 0 和相邻位置
                state_list = list(state)
                state_list[zero_pos], state_list[next_pos] = state_list[next_pos], state_list[zero_pos]
                next_state = ''.join(state_list)
                
                # 如果到达目标状态
                if next_state == target:
                    return steps + 1
                
                # 如果未访问过，加入队列
                if next_state not in visited:
                    visited.add(next_state)
                    queue.append((next_state, steps + 1))
        
        return -1

思路 1：复杂度分析

• 时间复杂度：$O((m \times n)! \times m \times n)$，状态总数为 $(m \times n)!$，每个状态需要 $O(m \times n)$ 时间处理。对于 $2 \times 3$ 的棋盘，状态数为 $6! = 720$。
• 空间复杂度：$O((m \times n)!)$，存储访问过的状态。