---

0782. 变为棋盘

• 标签：位运算、数组、数学、矩阵
• 难度：困难

题目链接

• 0782. 变为棋盘 - 力扣

题目大意

描述：

一个 $n \times n$ 的二维网络 $board$ 仅由 $0$ 和 $1$ 组成。每次移动，你能交换任意两列或是两行的位置。

要求：

返回 将这个矩阵变为「棋盘」所需的最小移动次数 。如果不存在可行的变换，输出 $-1$。

说明：

• 「棋盘」是指任意一格的上下左右四个方向的值均与本身不同的矩阵。
• $n == board.length$。
• $n == board[i].length$。
• $2 \le n \le 30$。
• $board[i][j]$ 将只包含 $0$ 或 $1$。

示例：

• 示例 1：

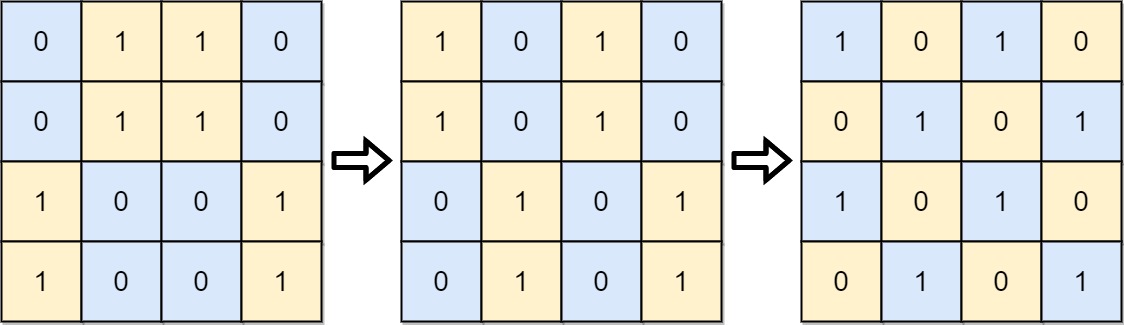
输入: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
输出: 2
解释:一种可行的变换方式如下，从左到右：
第一次移动交换了第一列和第二列。
第二次移动交换了第二行和第三行。

• 示例 2：

输入: board = [[0, 1], [1, 0]]
输出: 0
解释: 注意左上角的格值为0时也是合法的棋盘，也是合法的棋盘.

解题思路

思路 1：位运算 + 贪心

这道题要求将一个 $n \times n$ 的 01 矩阵通过交换行或列变成棋盘（相邻格子值不同）。

棋盘的性质：

1. 只有两种不同的行（或列）模式，且它们互补（0 和 1 互换）。
2. 这两种行（或列）的数量相差不超过 1。
3. 每一行（或列）中 0 和 1 的数量相差不超过 1。

算法步骤：

1. 检查矩阵是否可以变成棋盘：
   • 检查第一行和其他行的关系，只能有两种模式。
   • 检查第一列和其他列的关系，只能有两种模式。
   • 检查 0 和 1 的数量是否满足条件。
2. 计算最少交换次数：
   • 对于行：计算将行变成 010101... 或 101010... 需要的交换次数，选择较小的。
   • 对于列：同样计算。
   • 如果 $n$ 是奇数，只有一种合法的目标模式。
3. 返回行和列的最少交换次数之和。

思路 1：代码

class Solution:
    def movesToChessboard(self, board: List[List[int]]) -> int:
        n = len(board)
        
        # 检查第一行和第一列
        row_mask = 0
        col_mask = 0
        for i in range(n):
            row_mask = (row_mask << 1) | board[0][i]
            col_mask = (col_mask << 1) | board[i][0]
        
        # 检查是否只有两种行模式
        row_cnt = {row_mask: 0, row_mask ^ ((1 << n) - 1): 0}
        for i in range(n):
            mask = 0
            for j in range(n):
                mask = (mask << 1) | board[i][j]
            if mask not in row_cnt:
                return -1
            row_cnt[mask] += 1
        
        # 检查是否只有两种列模式
        col_cnt = {col_mask: 0, col_mask ^ ((1 << n) - 1): 0}
        for j in range(n):
            mask = 0
            for i in range(n):
                mask = (mask << 1) | board[i][j]
            if mask not in col_cnt:
                return -1
            col_cnt[mask] += 1
        
        # 检查两种模式的数量是否合法
        if abs(row_cnt[row_mask] - row_cnt[row_mask ^ ((1 << n) - 1)]) > 1:
            return -1
        if abs(col_cnt[col_mask] - col_cnt[col_mask ^ ((1 << n) - 1)]) > 1:
            return -1
        
        # 检查第一行和第一列的 0 和 1 数量
        row_ones = bin(row_mask).count('1')
        col_ones = bin(col_mask).count('1')
        if row_ones < n // 2 or row_ones > (n + 1) // 2:
            return -1
        if col_ones < n // 2 or col_ones > (n + 1) // 2:
            return -1
        
        # 计算最少交换次数
        def min_swaps(mask, ones):
            """计算将 mask 变成棋盘模式的最少交换次数"""
            # 目标模式：010101... 或 101010...
            target1 = 0
            target2 = 0
            for i in range(n):
                if i % 2 == 0:
                    target1 = (target1 << 1) | 1
                    target2 = (target2 << 1) | 0
                else:
                    target1 = (target1 << 1) | 0
                    target2 = (target2 << 1) | 1
            
            diff1 = bin(mask ^ target1).count('1')
            diff2 = bin(mask ^ target2).count('1')
            
            # 如果 n 是奇数，只有一种合法模式
            if n % 2 == 1:
                if ones * 2 > n:
                    return diff1 // 2
                else:
                    return diff2 // 2
            else:
                return min(diff1, diff2) // 2
        
        row_swaps = min_swaps(row_mask, row_ones)
        col_swaps = min_swaps(col_mask, col_ones)
        
        return row_swaps + col_swaps

思路 1：复杂度分析

• 时间复杂度：$O(n^2)$，需要遍历整个矩阵检查合法性。
• 空间复杂度：$O(1)$，只使用常数额外空间。