---

0894. 所有可能的真二叉树

• 标签：树、递归、记忆化搜索、动态规划、二叉树
• 难度：中等

题目链接

• 0894. 所有可能的真二叉树 - 力扣

题目大意

描述：

给定一个整数 $n$。

要求：

请你找出所有可能含 $n$ 个节点的 真二叉树 ，并以列表形式返回。

说明：

• 答案中每棵树的每个节点都必须符合 $Node$.$val == 0$。
• 答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表。
• 「真二叉树」是一类二叉树，树中每个节点恰好有 0 或 2 个子节点。
• $1 \le n \le 20$。

示例：

• 示例 1：

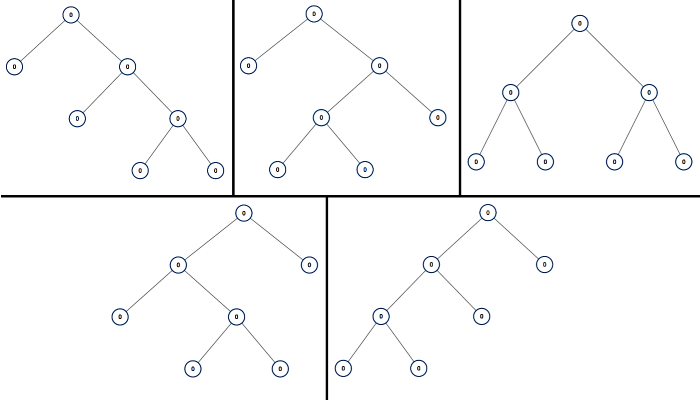
输入：n = 7
输出：[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

• 示例 2：

输入：n = 3
输出：[[0,0,0]]

解题思路

思路 1：递归 + 记忆化搜索

真二叉树的特点是每个节点要么有 0 个子节点（叶子节点），要么有 2 个子节点。因此，真二叉树的节点数必须是奇数。

关键观察：

• 如果 $n$ 是偶数，无法构成真二叉树，返回空列表。
• 如果 $n = 1$，只有一个节点，返回包含单个节点的列表。
• 如果 $n > 1$，根节点占 1 个节点，剩余 $n-1$ 个节点分配给左右子树。
• 左子树可以有 $1, 3, 5, \ldots, n-2$ 个节点，相应地右子树有 $n-2, n-4, \ldots, 1$ 个节点。

算法步骤：

1. 使用记忆化搜索避免重复计算。
2. 递归构建所有可能的左右子树组合。
3. 对于每种组合，创建一个新的根节点，连接左右子树。

思路 1：代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def allPossibleFBT(self, n: int) -> List[Optional[TreeNode]]:
        # 记忆化字典
        memo = {}
        
        def helper(n):
            """返回所有可能的 n 个节点的真二叉树"""
            # 如果已经计算过，直接返回
            if n in memo:
                return memo[n]
            
            # 偶数个节点无法构成真二叉树
            if n % 2 == 0:
                return []
            
            # 只有一个节点
            if n == 1:
                return [TreeNode(0)]
            
            result = []
            
            # 枚举左子树的节点数（必须是奇数）
            for left_count in range(1, n, 2):
                right_count = n - 1 - left_count
                
                # 递归构建所有可能的左右子树
                left_trees = helper(left_count)
                right_trees = helper(right_count)
                
                # 组合所有可能的左右子树
                for left in left_trees:
                    for right in right_trees:
                        root = TreeNode(0)
                        root.left = left
                        root.right = right
                        result.append(root)
            
            memo[n] = result
            return result
        
        return helper(n)

思路 1：复杂度分析

• 时间复杂度：$O(2^n)$，生成所有可能的真二叉树需要指数时间。
• 空间复杂度：$O(2^n)$，需要存储所有可能的树结构。