---

0812. 最大三角形面积

• 标签：几何、数组、数学
• 难度：简单

题目链接

• 0812. 最大三角形面积 - 力扣

题目大意

描述：

给定一个由 X-Y 平面上的点组成的数组 $points$，其中 $points[i] = [xi, yi]$。

要求：

从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 $10^{-5}$ 内的答案将会视为正确答案。

说明：

• $3 \le points.length \le 50$。
• $-50 \le xi, yi \le 50$。
• 给出的所有点「互不相同」。

示例：

• 示例 1：

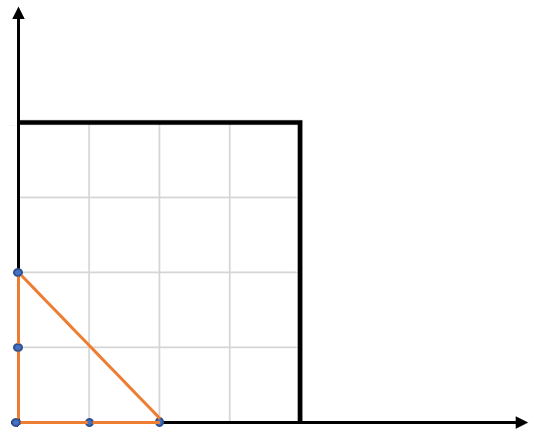
输入：points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出：2.00000
解释：输入中的 5 个点如上图所示，红色的三角形面积最大。

• 示例 2：

输入：points = [[1,0],[0,0],[0,1]]
输出：0.50000

解题思路

思路 1：枚举 + 几何

这道题要求计算由给定点组成的最大三角形面积。

对于三个点 $(x_1, y_1)$、$(x_2, y_2)$、$(x_3, y_3)$，三角形的面积可以用以下公式计算（鞋带公式）：

$$S = \frac{1}{2} |x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)|$$

算法步骤：

1. 枚举所有可能的三个点的组合。
2. 对于每个组合，使用鞋带公式计算三角形面积。
3. 记录最大面积。

思路 1：代码

class Solution:
    def largestTriangleArea(self, points: List[List[int]]) -> float:
        n = len(points)
        max_area = 0
        
        # 枚举所有可能的三个点
        for i in range(n):
            for j in range(i + 1, n):
                for k in range(j + 1, n):
                    # 获取三个点的坐标
                    x1, y1 = points[i]
                    x2, y2 = points[j]
                    x3, y3 = points[k]
                    
                    # 使用鞋带公式计算三角形面积
                    area = 0.5 * abs(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2))
                    
                    # 更新最大面积
                    max_area = max(max_area, area)
        
        return max_area

思路 1：复杂度分析

• 时间复杂度：$O(n^3)$，其中 $n$ 是点的数量。需要枚举所有三个点的组合。
• 空间复杂度：$O(1)$，只使用常数额外空间。