---

0840. 矩阵中的幻方

• 标签：数组、哈希表、数学、矩阵
• 难度：中等

题目链接

• 0840. 矩阵中的幻方 - 力扣

题目大意

描述：

$3 \times 3$ 的幻方是一个填充有 从 1 到 9 的不同数字的 $3 \times 3$ 矩阵，其中每行，每列以及两条对角线上的各数之和都相等。

给定一个由整数组成的 $row \times col$ 的 $grid$。

要求：

计算其中有多少个 $3 \times 3$ 的「幻方」子矩阵。

注意：虽然幻方只能包含 1 到 9 的数字，但 $grid$ 可以包含最多 15 的数字。

说明：

• $row == grid.length$。
• $col == grid[i].length$。
• $1 \le row, col \le 10$。
• $0 \le grid[i][j] \le 15$。

示例：

• 示例 1：

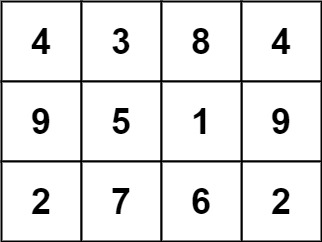
输入: grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]
输出: 1
解释: 
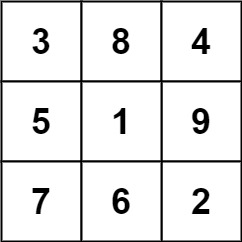
下面的子矩阵是一个 3 x 3 的幻方：

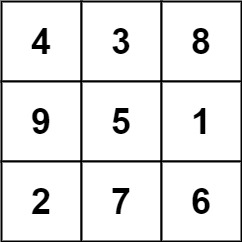
而这一个不是：

总的来说，在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。

• 示例 2：

输入: grid = [[8]]
输出: 0

解题思路

思路 1：枚举 + 模拟

这道题要求统计矩阵中 $3 \times 3$ 幻方的数量。幻方需要满足：

1. 包含 $1$ 到 $9$ 的所有数字，且每个数字只出现一次。
2. 每行、每列、两条对角线的和都相等（都等于 $15$）。

算法步骤：

1. 枚举所有可能的 $3 \times 3$ 子矩阵的左上角位置。
2. 对于每个子矩阵，检查是否为幻方：
   • 检查是否包含 $1$ 到 $9$ 的所有数字。
   • 检查每行、每列、两条对角线的和是否都等于 $15$。
3. 统计满足条件的幻方数量。

思路 1：代码

class Solution:
    def numMagicSquaresInside(self, grid: List[List[int]]) -> int:
        def is_magic(square):
            # 检查是否为幻方
            # 1. 检查是否包含 1 到 9 的所有数字
            nums = []
            for row in square:
                for num in row:
                    if num < 1 or num > 9:
                        return False
                    nums.append(num)
            
            if sorted(nums) != list(range(1, 10)):
                return False
            
            # 2. 检查每行、每列、两条对角线的和是否都等于 15
            # 检查行
            for row in square:
                if sum(row) != 15:
                    return False
            
            # 检查列
            for col in range(3):
                if sum(square[row][col] for row in range(3)) != 15:
                    return False
            
            # 检查对角线
            if sum(square[i][i] for i in range(3)) != 15:
                return False
            if sum(square[i][2 - i] for i in range(3)) != 15:
                return False
            
            return True
        
        rows = len(grid)
        cols = len(grid[0])
        count = 0
        
        # 枚举所有可能的 3x3 子矩阵
        for i in range(rows - 2):
            for j in range(cols - 2):
                # 提取 3x3 子矩阵
                square = [grid[i + r][j:j + 3] for r in range(3)]
                if is_magic(square):
                    count += 1
        
        return count

思路 1：复杂度分析

• 时间复杂度：$O(m \times n)$，其中 $m$ 和 $n$ 分别是矩阵的行数和列数。需要枚举所有可能的 $3 \times 3$ 子矩阵，每个子矩阵的检查时间为常数。
• 空间复杂度：$O(1)$，只使用常数额外空间。