---

0807. 保持城市天际线

• 标签：贪心、数组、矩阵
• 难度：中等

题目链接

• 0807. 保持城市天际线 - 力扣

题目大意

描述：

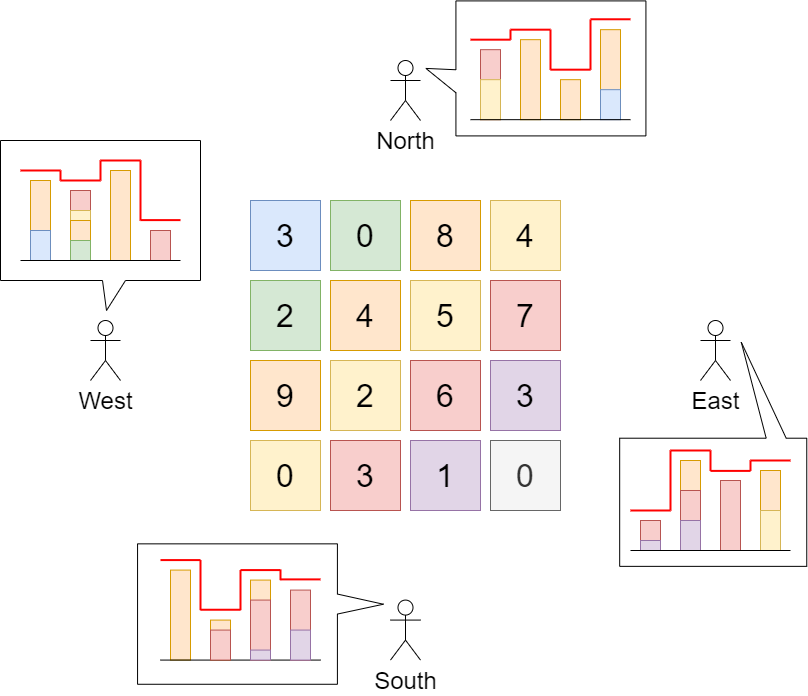
给定一座由 $n \times n$ 个街区组成的城市，每个街区都包含一座立方体建筑。给你一个下标从 0 开始的 $n \times n$ 整数矩阵 $grid$，其中 $grid[r][c]$ 表示坐落于 $r$ 行 $c$ 列的建筑物的「高度」。

城市的「天际线」是从远处观察城市时，所有建筑物形成的外部轮廓。从东、南、西、北四个主要方向观测到的「天际线」可能不同。

我们被允许为「任意数量的建筑物」的高度增加「任意增量（不同建筑物的增量可能不同）」。高度为 0 的建筑物的高度也可以增加。然而，增加的建筑物高度「不能影响」从任何主要方向观察城市得到的「天际线」。

要求：

在「不改变」从任何主要方向观测到的城市「天际线」的前提下，返回建筑物可以增加的「最大高度增量总和」。

说明：

• $n == grid.length$。
• $n == grid[r].length$。
• $2 \le n \le 50$。
• $0 \le grid[r][c] \le 10^{3}$。

示例：

• 示例 1：

输入：grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
输出：35
解释：建筑物的高度如上图中心所示。
用红色绘制从不同方向观看得到的天际线。
在不影响天际线的情况下，增加建筑物的高度：
gridNew = [ [8, 4, 8, 7],
            [7, 4, 7, 7],
            [9, 4, 8, 7],
            [3, 3, 3, 3] ]

• 示例 2：

输入：grid = [[0,0,0],[0,0,0],[0,0,0]]
输出：0
解释：增加任何建筑物的高度都会导致天际线的变化。

解题思路

思路 1：贪心 + 矩阵

这道题要求在不改变天际线的前提下，计算建筑物可以增加的最大高度增量总和。

关键观察：

• 从东西方向看，天际线由每行的最大值决定。
• 从南北方向看，天际线由每列的最大值决定。
• 对于位置 $(i, j)$ 的建筑物，它的最大高度不能超过第 $i$ 行的最大值和第 $j$ 列的最大值中的较小值。

算法步骤：

1. 计算每行的最大值 $row\_max[i]$。
2. 计算每列的最大值 $col\_max[j]$。
3. 对于每个位置 $(i, j)$，建筑物可以增加的高度为 $\min(row\_max[i], col\_max[j]) - grid[i][j]$。
4. 累加所有位置的增量。

思路 1：代码

class Solution:
    def maxIncreaseKeepingSkyline(self, grid: List[List[int]]) -> int:
        n = len(grid)
        
        # 计算每行的最大值
        row_max = [max(grid[i]) for i in range(n)]
        
        # 计算每列的最大值
        col_max = [max(grid[i][j] for i in range(n)) for j in range(n)]
        
        # 计算总增量
        total_increase = 0
        for i in range(n):
            for j in range(n):
                # 当前位置的最大高度
                max_height = min(row_max[i], col_max[j])
                # 累加增量
                total_increase += max_height - grid[i][j]
        
        return total_increase

思路 1：复杂度分析

• 时间复杂度：$O(n^2)$，其中 $n$ 是矩阵的边长。需要遍历矩阵计算行列最大值和增量。
• 空间复杂度：$O(n)$，需要存储每行和每列的最大值。