---

0849. 到最近的人的最大距离

• 标签：数组
• 难度：中等

题目链接

• 0849. 到最近的人的最大距离 - 力扣

题目大意

描述：

给定一个数组 $seats$ 表示一排座位，其中 $seats[i] = 1$ 代表有人坐在第 i 个座位上，$seats[i] = 0$ 代表座位 $i$ 上是空的（下标从 0 开始）。

至少有一个空座位，且至少有一人已经坐在座位上。

亚历克斯希望坐在一个能够使他与离他最近的人之间的距离达到最大化的座位上。

要求：

返回他到离他最近的人的最大距离。

说明：

• $2 \le seats.length \le 2 * 10^{4}$。
• $seats[i]$ 为 0 或 1。
• 至少有一个「空座位」。
• 至少有一个「座位上有人」。

示例：

• 示例 1：

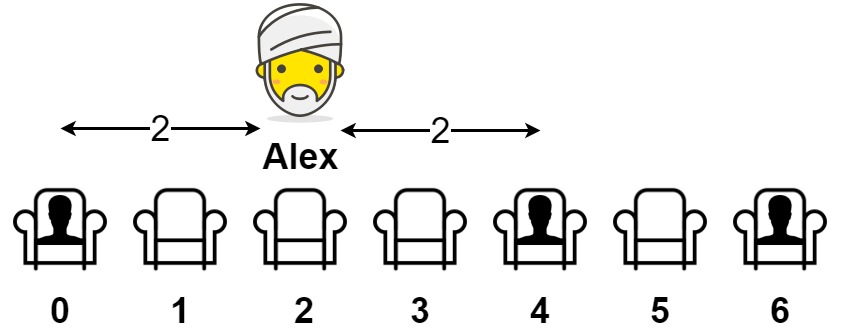
输入：seats = [1,0,0,0,1,0,1]
输出：2
解释：
如果亚历克斯坐在第二个空位（seats[2]）上，他到离他最近的人的距离为 2 。
如果亚历克斯坐在其它任何一个空位上，他到离他最近的人的距离为 1 。
因此，他到离他最近的人的最大距离是 2 。

• 示例 2：

输入：seats = [1,0,0,0]
输出：3
解释：
如果亚历克斯坐在最后一个座位上，他离最近的人有 3 个座位远。
这是可能的最大距离，所以答案是 3 。

解题思路

思路 1：一次遍历

这道题要求找到使亚历克斯到最近的人的距离最大化的座位。

关键观察：

• 最大距离可能出现在三种情况：
  1. 两个有人座位之间的中点。
  2. 最左边的空座位（如果最左边是空的）。
  3. 最右边的空座位（如果最右边是空的）。

算法步骤：

1. 遍历座位数组，记录上一个有人座位的位置 $prev$。
2. 对于每个空座位：
   • 如果 $prev == -1$（左边没有人），距离为当前位置到第一个有人座位的距离。
   • 否则，距离为 $(i - prev) // 2$（两个有人座位之间的中点）。
3. 特殊处理最右边的空座位。
4. 返回最大距离。

思路 1：代码

class Solution:
    def maxDistToClosest(self, seats: List[int]) -> int:
        n = len(seats)
        max_dist = 0
        prev = -1  # 上一个有人座位的位置
        
        for i in range(n):
            if seats[i] == 1:
                # 如果当前座位有人
                if prev == -1:
                    # 如果左边没有人，距离为从开始到当前位置
                    max_dist = i
                else:
                    # 否则，距离为两个有人座位之间的中点
                    max_dist = max(max_dist, (i - prev) // 2)
                prev = i
        
        # 特殊处理最右边的空座位
        max_dist = max(max_dist, n - 1 - prev)
        
        return max_dist

思路 1：复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是座位数组的长度。只需遍历一次数组。
• 空间复杂度：$O(1)$，只使用常数额外空间。