0864. 获取所有钥匙的最短路径

ITCharge大约 3 分钟

---

0864. 获取所有钥匙的最短路径

标签：位运算、广度优先搜索、数组、矩阵
难度：困难

题目链接

0864. 获取所有钥匙的最短路径 - 力扣

题目大意

描述：

给定一个二维网格 $grid$ ，其中：

'.' 代表一个空房间
'#' 代表一堵墙
'@' 是起点
小写字母代表钥匙
大写字母代表锁

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 $k$ 为钥匙/锁的个数，且满足 $1 \le k \le 6$ ，字母表中的前 $k$ 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

要求：

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1。

说明：

$m == grid.length$ 。
$n == grid[i].length$ 。
$1 \le m, n \le 30$ 。
$grid[i][j]$ 只含有 '.', '#', '@', 'a'-'f' 以及 'A'-'F'。
钥匙的数目范围是 $[1, 6]$ 。
每个钥匙都对应一个「不同」的字母。
每个钥匙正好打开一个对应的锁。

示例：

示例 1：

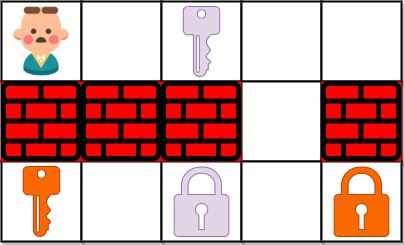
输入：grid = ["@.a..","###.#","b.A.B"]
输出：8
解释：目标是获得所有钥匙，而不是打开所有锁。

示例 2：

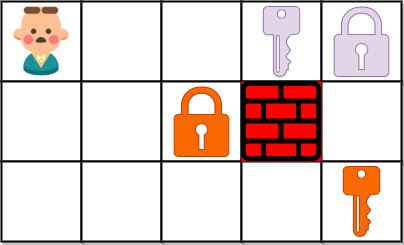
输入：grid = ["@..aA","..B#.","....b"]
输出：6

解题思路

思路 1:BFS + 状态压缩

这是一个带状态的最短路径问题。状态包括:当前位置 $(x, y)$ 和已收集的钥匙集合。

由于钥匙最多 6 个，可以用 6 位二进制数表示钥匙的收集状态，第 $i$ 位为 1 表示已收集第 $i$ 把钥匙。

算法步骤:

找到起点位置和钥匙总数
使用 BFS，状态为 $(x, y, keys)$ ，其中 $keys$ 是钥匙的二进制状态
对于每个状态,尝试向四个方向移动:
- 如果是墙，不能通过
- 如果是锁，需要有对应的钥匙才能通过
- 如果是钥匙，收集它并更新状态
当收集到所有钥匙时，返回步数

思路 1:代码

class Solution:
    def shortestPathAllKeys(self, grid: List[str]) -> int:
        from collections import deque
        
        m, n = len(grid), len(grid[0])
        start_x, start_y = 0, 0
        key_count = 0
        
        # 找到起点和钥匙总数
        for i in range(m):
            for j in range(n):
                if grid[i][j] == '@':
                    start_x, start_y = i, j
                elif grid[i][j].islower():
                    key_count += 1
        
        # 所有钥匙都收集完的状态
        all_keys = (1 << key_count) - 1
        
        # BFS
        queue = deque([(start_x, start_y, 0, 0)])  # (x, y, keys, steps)
        visited = set()
        visited.add((start_x, start_y, 0))
        
        directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
        
        while queue:
            x, y, keys, steps = queue.popleft()
            
            # 如果收集到所有钥匙,返回步数
            if keys == all_keys:
                return steps
            
            # 尝试四个方向
            for dx, dy in directions:
                nx, ny = x + dx, y + dy
                
                # 检查边界
                if nx < 0 or nx >= m or ny < 0 or ny >= n:
                    continue
                
                cell = grid[nx][ny]
                
                # 如果是墙,跳过
                if cell == '#':
                    continue
                
                # 如果是锁,检查是否有钥匙
                if cell.isupper():
                    key_bit = ord(cell.lower()) - ord('a')
                    if not (keys & (1 << key_bit)):
                        continue
                
                # 更新钥匙状态
                new_keys = keys
                if cell.islower():
                    key_bit = ord(cell) - ord('a')
                    new_keys = keys | (1 << key_bit)
                
                # 如果状态未访问过,加入队列
                if (nx, ny, new_keys) not in visited:
                    visited.add((nx, ny, new_keys))
                    queue.append((nx, ny, new_keys, steps + 1))
        
        return -1

思路 1:复杂度分析

时间复杂度: $O(m \times n \times 2^k)$ ,其中 $m$ 和 $n$ 是网格的大小, $k$ 是钥匙的数量。每个状态最多访问一次。
空间复杂度: $O(m \times n \times 2^k)$ ,需要存储访问状态。