---

0885. 螺旋矩阵 III

• 标签：数组、矩阵、模拟
• 难度：中等

题目链接

• 0885. 螺旋矩阵 III - 力扣

题目大意

描述：

在 $rows \times cols$ 的网格上，你从单元格 $(rStart, cStart)$ 面朝东面开始。网格的西北角位于第一行第一列，网格的东南角位于最后一行最后一列。

你需要以顺时针按螺旋状行走，访问此网格中的每个位置。每当移动到网格的边界之外时，需要继续在网格之外行走（但稍后可能会返回到网格边界）。

最终，我们到过网格的所有 $rows \times cols$ 个空间。

要求：

按照访问顺序返回表示网格位置的坐标列表。

说明：

• $1 \le rows, cols \le 10^{3}$。
• $0 \le rStart \lt rows$。
• $0 \le cStart \lt cols$。

示例：

• 示例 1：

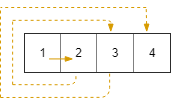
输入：rows = 1, cols = 4, rStart = 0, cStart = 0
输出：[[0,0],[0,1],[0,2],[0,3]]

• 示例 2：

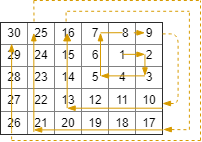
输入：rows = 5, cols = 6, rStart = 1, cStart = 4
输出：[[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

解题思路

思路 1:模拟

按照螺旋顺序模拟机器人的行走过程:

1. 螺旋行走的规律是:向右走 1 步,向下走 1 步,向左走 2 步,向上走 2 步,向右走 3 步,向下走 3 步...
2. 可以发现,每个方向走的步数规律为:1, 1, 2, 2, 3, 3, 4, 4...
3. 方向顺序为:东、南、西、北,循环往复。
4. 在行走过程中,如果当前位置在网格内,就将其加入结果。
5. 当结果数组的长度等于 $rows \times cols$ 时,说明已经访问完所有格子。

思路 1:代码

class Solution:
    def spiralMatrixIII(self, rows: int, cols: int, rStart: int, cStart: int) -> List[List[int]]:
        # 方向数组:东、南、西、北
        directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        
        result = [[rStart, cStart]]  # 起始位置
        if rows * cols == 1:
            return result
        
        r, c = rStart, cStart
        steps = 1  # 当前方向要走的步数
        
        while len(result) < rows * cols:
            # 每两个方向,步数增加 1
            for i in range(4):
                dr, dc = directions[i]
                # 在当前方向走 steps 步
                for _ in range(steps):
                    r += dr
                    c += dc
                    # 如果在网格内,加入结果
                    if 0 <= r < rows and 0 <= c < cols:
                        result.append([r, c])
                        if len(result) == rows * cols:
                            return result
                
                # 每走完两个方向,步数加 1
                if i % 2 == 1:
                    steps += 1
        
        return result

思路 1:复杂度分析

• 时间复杂度:$O(\max(rows, cols)^2)$,最坏情况下需要走出网格很远才能访问完所有格子。
• 空间复杂度:$O(1)$,不考虑结果数组的空间。