0913. 猫和老鼠

ITCharge大约 4 分钟

---

0913. 猫和老鼠

标签：图、拓扑排序、记忆化搜索、数学、动态规划、博弈
难度：困难

题目链接

0913. 猫和老鼠 - 力扣

题目大意

描述：

两位玩家分别扮演猫和老鼠，在一张「无向」图上进行游戏，两人轮流行动。

图的形式是： $graph[a]$ 是一个列表，由满足 $ab$ 是图中的一条边的所有节点 $b$ 组成。

老鼠从节点 1 开始，第一个出发；猫从节点 2 开始，第二个出发。在节点 0 处有一个洞。

在每个玩家的行动中，他们必须沿着图中与所在当前位置连通的一条边移动。例如，如果老鼠在节点 1 ，那么它必须移动到 $graph[1]$ 中的任一节点。

此外，猫无法移动到洞中（节点 0）。

然后，游戏在出现以下三种情形之一时结束：

如果猫和老鼠出现在同一个节点，猫获胜。
如果老鼠到达洞中，老鼠获胜。
如果某一位置重复出现（即，玩家的位置和移动顺序都与上一次行动相同），游戏平局。

给定一张图 $graph$ ，并假设两位玩家都都以最佳状态参与游戏。

要求：

如果老鼠获胜，则返回 1；
如果猫获胜，则返回 2；
如果平局，则返回 0 。

说明：

$3 \le graph.length \le 50$ 。
$1 \le graph[i].length \lt graph.length$ 。
$0 \le graph[i][j] \lt graph.length$ 。
$graph[i][j] \ne i$ 。
$graph[i]$ 互不相同。
猫和老鼠在游戏中总是可以移动。

示例：

示例 1：

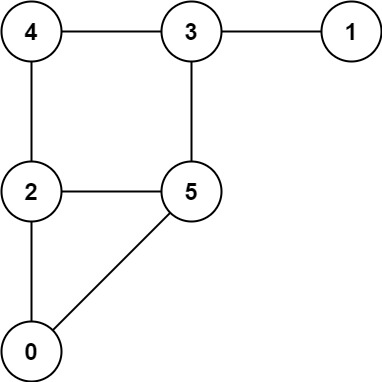
输入：graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
输出：0

示例 2：

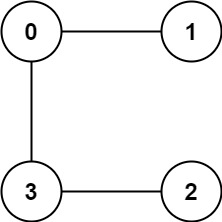
输入：graph = [[1,3],[0],[3],[0,2]]
输出：1

解题思路

思路 1：博弈论 + 拓扑排序

思路

这是一个博弈问题，需要判断在双方都采取最优策略的情况下，谁会获胜。

我们可以使用 拓扑排序 + 博弈状态 来解决：

状态定义： $(mouse, cat, turn)$ 表示老鼠在位置 $mouse$ ，猫在位置 $cat$ ，当前轮到 $turn$ （ $1$ 表示老鼠， $2$ 表示猫）。
状态结果：
- $0$ ：平局
- $1$ ：老鼠获胜
- $2$ ：猫获胜

使用逆向思维，从已知结果的状态开始，逐步推导其他状态：

初始化必胜/必败状态：
- 老鼠到达洞口（ $mouse = 0$ ）：老鼠获胜。
- 猫抓到老鼠（ $mouse = cat$ ）：猫获胜。
拓扑排序：从已知状态出发，更新前驱状态：
- 如果某个状态的所有后继状态都对对手有利，则该状态对当前玩家不利。
- 如果某个状态存在一个后继状态对当前玩家有利，则该状态对当前玩家有利。
返回初始状态： $(1, 2, 1)$ 的结果。

代码

class Solution:
    def catMouseGame(self, graph: List[List[int]]) -> int:
        n = len(graph)
        DRAW, MOUSE_WIN, CAT_WIN = 0, 1, 2
        
        # 状态：(mouse, cat, turn)，turn=1 表示老鼠，turn=2 表示猫
        # 结果：0=平局，1=老鼠赢，2=猫赢
        result = [[[DRAW] * 3 for _ in range(n)] for _ in range(n)]
        degree = [[[0] * 3 for _ in range(n)] for _ in range(n)]
        
        # 计算每个状态的出度
        for mouse in range(n):
            for cat in range(n):
                degree[mouse][cat][1] = len(graph[mouse])
                degree[mouse][cat][2] = len([node for node in graph[cat] if node != 0])
        
        # 初始化队列：已知结果的状态
        from collections import deque
        queue = deque()
        
        for cat in range(n):
            for turn in [1, 2]:
                # 老鼠到达洞口，老鼠赢
                result[0][cat][turn] = MOUSE_WIN
                queue.append((0, cat, turn))
                # 猫抓到老鼠（但猫不能在洞口），猫赢
                if cat > 0:
                    result[cat][cat][turn] = CAT_WIN
                    queue.append((cat, cat, turn))
        
        # 拓扑排序
        while queue:
            mouse, cat, turn = queue.popleft()
            current_result = result[mouse][cat][turn]
            
            if turn == 1:  # 当前是老鼠的回合，推导上一步猫的状态
                for prev_cat in graph[cat]:
                    if prev_cat == 0:  # 猫不能进洞
                        continue
                    if result[mouse][prev_cat][2] != DRAW:
                        continue
                    
                    if current_result == CAT_WIN:
                        # 如果老鼠这步后猫赢，说明猫的上一步可以导致猫赢
                        result[mouse][prev_cat][2] = CAT_WIN
                        queue.append((mouse, prev_cat, 2))
                    else:
                        # 否则，减少出度
                        degree[mouse][prev_cat][2] -= 1
                        if degree[mouse][prev_cat][2] == 0:
                            # 所有后继状态都对猫不利，猫输
                            result[mouse][prev_cat][2] = MOUSE_WIN
                            queue.append((mouse, prev_cat, 2))
            else:  # 当前是猫的回合，推导上一步老鼠的状态
                for prev_mouse in graph[mouse]:
                    if result[prev_mouse][cat][1] != DRAW:
                        continue
                    
                    if current_result == MOUSE_WIN:
                        # 如果猫这步后老鼠赢，说明老鼠的上一步可以导致老鼠赢
                        result[prev_mouse][cat][1] = MOUSE_WIN
                        queue.append((prev_mouse, cat, 1))
                    else:
                        # 否则，减少出度
                        degree[prev_mouse][cat][1] -= 1
                        if degree[prev_mouse][cat][1] == 0:
                            # 所有后继状态都对老鼠不利，老鼠输
                            result[prev_mouse][cat][1] = CAT_WIN
                            queue.append((prev_mouse, cat, 1))
        
        return result[1][2][1]

复杂度分析

时间复杂度： $O(n^3)$ ，其中 $n$ 是图中节点的数量。需要遍历所有状态和边。
空间复杂度： $O(n^2)$ ，需要存储所有状态的结果和出度。